Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 54

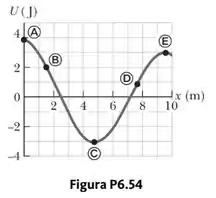
Para a curva da energia potencial mostrada na Figura P6.54,

a) determine se a força Fx é positiva, negativa ou zero nos cinco pontos indicados,

b) indique pontos de equilíbrio estável, instável e neutro,

c) esboce a curva de Fx por x de x = 0 a x = 9,5 m.

Passo 1

a)Por definição, a gente sabe que a força é o negativo da derivada da energia potencial, ou seja:

Logo, o sinal da inclinação da reta tangente ao gráfico nos pontos pedidos vai definir o sinal de . Vamos analisar:

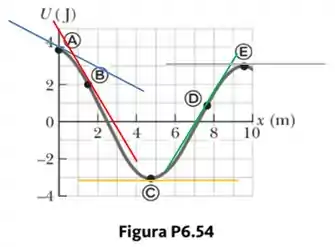
Pra A, sendo a reta tangente decrescente (desce da esquerda pra direita), a gente tem uma derivada negativa.

Se a derivada é negativa, e a gente acabou de ver que é o negativo da derivada pra essa função, então , nesse ponto, é positiva!

Pra B, a mesma coisa, né?! Então, mesmo raciocínio: vai ser positiva!
Em C, a gente tem ponto de mínimo, e, como você deve saber, nesses pontos a derivada é nula. Logo, também é nula!
Pra D, a inclinação da reta tangente já é positiva (cresce da esquerda pra direita), e, assim, a gente vai ter que fica negativa!
Finalmente, em E, ocorre o mesmo que em C: é ponto de máximo, logo, a derivada se anula, e vai ser nula também.

Passo 2

b)Os pontos de equilíbrio vão ser aqueles em que a força resultante é nula, logo, o corpo não muda de posição, a não ser que uma força externa aja sobre ele.

Assim, já dá pra gente verificar, no gráfico, que esses pontos são justamente os pontos de mínimo e máximo, C e E, respectivamente.

Pra saber se é ponto de equilíbrio estável ou instável, a dica é simples:

Imagina que o ponto C é o vale entre duas montanhas. Se você chuta uma bola montanha acima, ela vai subir as “paredes” da montanha até uma determinada altura e, prontamente, vai voltar à posição inicial C, né?

Esse é o caso de um ponto de equilíbrio estável, porque a bola tenderia a retornar a ele após uma variação na sua posição, ou seja, uma variação da sua energia potencial.

Já pra E, é justamente o oposto: se você tem uma bola no topo de uma montanha, que imaginamos ser o ponto E, e se você chuta ela desse ponto, ela cai, e não tende a voltar mais pra E! Esse é um caso de ponto de equilíbrio instável!

Com isso a gente conclui que os pontos de mínimo são sempre pontos de equilíbrio estável, e os de máximo são pontos de equilíbrio instável.

Agora, quanto aos neutros? São pontos em que o equilíbrio ocorreria de modo “igual”. Imagina o chão da sua casa. Pensa na cadeira do seu PC. Ela não tá paradinha ali? Agora arrasta ela mentalmente. Ela continuou parada, ou saiu correndo de volta pra posição inicial que estava?

Certamente ficou parada! Esse é um caso de equilíbrio neutro, ok?!

No caso desse gráfico, a gente não tem nenhum ponto desse tipo, já que, se uma bola fosse colocada em A, B ou D, ela tenderia a cair pra C.

Resposta

Vide Passos 1 e 2.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de 250g é deixado cair em uma mola vertical, inicialmente relaxada, cuja constante elástica é k = 2,5N / c m (Fig. 7-44). O bloco fica acoplado à mola, comprimindo-a em 12c m até parar moment

Uma mola com um ponteiro está pendurada perto de uma régua graduada em milímetros. Três pacotes diferentes são pendurados na mola, um de cada vez, como mostra a Fig. 7-46. (a) Qual é a marca da régua

Uma bola de gude move-se ao longo do eixo Ox. A energia potencial é indicada na Figura 7.28. a) Para quais valores de x indicados no gráfico a força é igual a zero? b) Para quais valores de x indicado

Um dispositivo experimental que se desloca no plano xy é submetido à ação de uma força que produz uma função energia potencial dada por U ( x . y ) = k ( x ² + y ² ) + k ' x y ² ² , onde k e k’ são co

Um objeto se desloca no plano xy submetido à ação de uma força conservativa descrita pela função energia potencial dada por U ( x , y ) = α ( 1 x ² + 1 y ² ) ² ² , onde α é uma constante positiva.Dedu