Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 7.Problemas Adicionais - Ex. 71

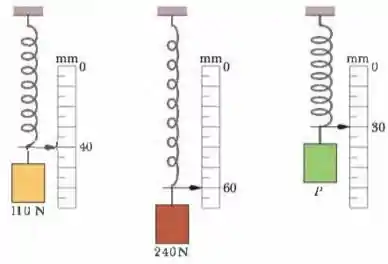
Uma mola com um ponteiro está pendurada perto de uma régua graduada em milímetros. Três pacotes diferentes são pendurados na mola, um de cada vez, como mostra a Fig. 7-46. (a) Qual é a marca da régua indicada pelo ponteiro quando não há nenhum pacote pendurado na mola? (b) Qual é o peso do terceiro pacote?

Passo 1

Podemos expressar a força elástica exercida pela mola sobre a caixa atravás da lei de Hooke:

Assim, podemos escrever para as duas primeiras caixas:

Passo 2

Portanto, para determinar a marca da régua quando não há nenhum pacote, devemos resolver esse sisteminha acima. Isolando o na primeira equação:

Substiuindo na segunda:

Assim reescrevendo a equação:

Isolando :

Passo 3

Para determinar o valor do P da terceira caixa, devemos escrever a lei de Hooke, considerando que ela está em equilíbrio, portanto, . Assim:

Podemos obter usando a expressão , portanto, substituindo na equação acima:

Resposta

;
.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A energia potencial de uma molécula diatômica (um sistema de dois átomos, como H2 ou O2) é dada por U = A r 12 - B r 6 onde r é a distância entre os átomos da molécula e A e B são constantes positivas

Uma única força conservativa F ( x ) age sobre uma partícula de 1,0k g que se move ao longo de um eixo x . A energia potencial U ( x ) associada a F ( x ) é dada por U x = - 4 x e - x 4J onde x está e

A Fig. 8-48 mostra um gráfico da energia potencial U em função da posição x para uma partícula de 0,90k g que pode se deslocar apenas ao longo de um eixo x . (Forças dissipativas não estão envolvidas.

Com o arranjo de forças do Problema 81, uma partícula de 2,00k g é liberada em x=5,00m , com uma velocidade de 3,45m / s , no sentido negativo do eixox . (a) Se a partícula pode chegar ao ponto x=0m ,

Dê um exemplo de uma partícula que tem energia cinética constante mas está acelerada. Pode uma partícula não acelerada ter energia cinética variável? Caso afirmativo, dê um exemplo.