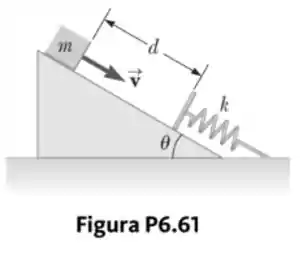
Um plano inclinado de ângulo = 20,0° tem uma mola de constante elástica k = 500 N/m presa firmemente na parte inferior, de maneira que a mola fica paralela à superfície, como mostrado previamente na Figura P6.61. Um bloco de massa m = 2,50 kg é colocado sobre o plano a uma distância d = 0,300 m da mola. Dessa posição, o bloco é projetado para baixo na direção da mola com velocidade escalar v = 0,750 m/s. Por qual distância a mola é comprimida quando o bloco momentaneamente entra em repouso?

Questão tranquila, chuchus! Dá pra gente resolver pela conservação da energia do sistema.

A situação inicial que a gente tem é o bloquinho com uma certa altura – logo, com uma certa energia potencial – e com uma velocidade de – logo, com uma determinada energia cinética.

Bora começar determinando qual a altura que o bloco tá nesse começo, que daí a gente determina a energia potencial. Pra isso, a gente pode partir de , uma vez que a gente tem a “hipotenusa”, que vale a distância percorrida, de .

Nisso, a gente tem:

Beleza? Com isso a gente já tem os dados pra determinar a energia potencial do bloco, que vale:

Considerando , a gente tem:

Legal! Agora, pra energia cinética a gente vai ter:

Aplicando os nossos dados, temos:

Com isso, a energia mecânica, que é o somatório dessas energias, nessa situação vale