48. Um carrinho de montanha-russa está se movendo com rapidez no início do percurso, quando desce um vale de e depois sobe até o topo de uma elevação, acima do início do percurso. Desconsidere o atrito e a resistência do ar.
(a) Qual a menor rapidez necessária para que o carrinho ultrapasse o topo da elevação?
(b) Esta rapidez pode ser alterada modificando-se a profundidade do vale, para que o carrinho adquira mais rapidez lá embaixo? Explique.
Passo 1
Olhando o enunciado, tudo parece meio confuso. O carrinho desce até o vale e depois sobe? Vamos descolar uma imagem, pra ajudar a entender esse raio de problema:
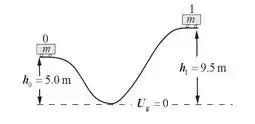
Agora sim as coisas estão começando a ficar mais claras!
Considerando o sistema de nossa análise como o conjunto montanha-russa, carrinho e a Terra e denotando a posição inicial com o número e a posição final, na parte superior da segunda colina, com o numeral ; podemos usar o teorema de trabalho e energia para relacionar as energias da montanha-russa em suas posições inicial e final. Seja a massa do montanha russa.
Mas acho que estamos esquecendo alguma coisa! O que será?
Lembrei! Falta definir qual será o nosso zero de potencial gravitacional. Bom! Vamos escolher o referencial que seja mais convenientes para nossos cálculos, que olhando bem a figura acima, só pode ser o solo! Vamos fazer, enfim, nossas contas.
Passo 2
(a) Aplicando o teorema trabalho e energia para o nosso sistema, onde é a notação de energia cinética, é a notação de energia potencial e é o trabalho da força externa chegamos a:
Mas como , uma vez que não há forças externas agindo no nosso sistema, temos que:
Só que e , nada mais são do que a diferença entre as energias finale e inicial e ). Com isso, obtemos que:
Agora vamos parar um pouco as contas para analisar com calma o nosso problema. Como descrito no enunciado, no instante inicial o carrinho está descendo um vale numa altura acima da origem, movendo-se com uma velocidade . É aí que vem o grande xissss da questão. O enunciado pede a menor velocidade necessária para que o carrinho ultrapasse o topo da elevação. Ora bolas, a menor velocidade , vai ocorrer na situação em que não há nenhuma velocidade no topo da elevação , havendo apenas energia potencial nesse instante. Ou seja vai ser igual a zero.
Substituindo as fórmulas relativas a cada tipo de energia, chegamos a:
Cancela-se a massa e isola-se o :
Aí sim! Chegamos à formula pelo qual tanto batalhamos. Resta só substituir os valores numéricos correspondentes:
Passo 3
(b) Bom! Essa é uma pergunta um tanto quanto traiçoeira. Mas vamos dar uma olhada na equação para que encontramos lá no :
Olhando essa fórmula percebemos que a velocidade necessária depende apenas da diferença de altura entre as duas elevações. Logo modificar a profundidade do vale não muda nada. Captou !
Resposta
a)
b) Não