Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 60
Em física, é importante utilizar aproximações matemáticas.
a) Demonstre que para ângulos pequenos () em que está em radianos e em graus.
b) Utilize uma calculadora para encontrar o maior ângulo para o qual pode ser aproximada por a com um erro menor que .
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
A tabela abaixo mostra em graus, em radianos, para ângulos de 150° a 31.1°:
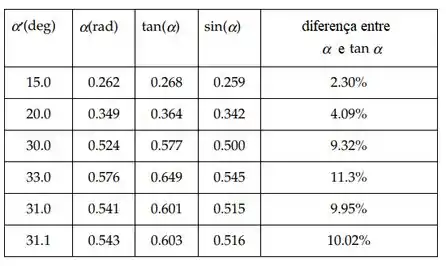
Vemos que em radianos, começam juntos do zero e divergem apenas ligeiramente para ângulos pequenos. Assim é o maior ângulo para o qual
Resposta
é o maior ângulo para o qual
Exercícios de Livros Relacionados
Um aluno usa um metro para medir a espessura de um livro e obtém 4,3c m±0,1c m . Outros alunos medem a espessura com o paquímetro de vernier e obtêm quatro medidas diferentes: 4,32c m±0,01c m 4,31c m±
O raio de uma esfera sólida uniforme é medido como ( 6,50 ± 0,20 )c m e sua massa como ( 1,85 ± 0,02 )k g . Determine a densidade da esfera em quilogramas por metro cúbico e a incerteza da densidade.O
Uma calçada deve ser construída ao redor de uma piscina que mede ( 10,0 ± 0,1 )m por ( 17,0 ± 0,1 )m . Se a calçada medir ( 1,00 ± 0,01 )m de largura por ( 9,0 ± 0,1 )c m de espessura, qual será o vol
Há quase π × 10 7s em um ano. Encontre o erro de porcentagem nessa aproximação, em que o “erro de porcentagem” é definido como: e r r od ep o r c e n t a g e m = v a l o rp r e s u m i d o - v a l o r