Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 25
Uma calçada deve ser construída ao redor de uma piscina que mede por . Se a calçada medir de largura por de espessura, qual será o volume de concreto necessário e qual a incerteza aproximada desse volume?
Observação: O Apêndice B.8 do livro sobre propagação de incerteza pode ser útil na resolução desse problema.
Passo 1
Fala ai galera, mais uma questão de incerteza, bora resolver?
Antes de começarmos, vamos entender a questão através da imagem a seguir.
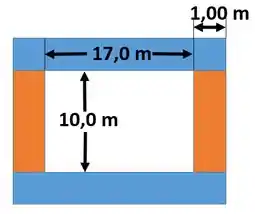
O objetivo é calcularmos o volume do concreto ao redor da piscina. Para isso vamos resolver por etapas.
Na primeira etapa iremos calcular o volume total e na segunda etapa vamos calcular a incerteza da medida do volume total.
SIMBORA!
Cálculo de :
Cálculo de :
Cálculo do volume total ():
Passo 2
A vamos calcular a incerteza da medida do volume total. De acordo com o apêndice B8 “Quando medidas com incertezas são divididas ou multiplicadas, devemos adicionar as incertezas absolutas para obter incerteza absoluta no resultado.”
Para encontrar o volume total foi feito o produto entre o valor do comprimento, largura e altura. Sendo assim será necessário descobrirmos as incertezas de tais medidas.
Agora como diz a regra, devemos somar tais incertezas.
Portanto o Volume total é