Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 50

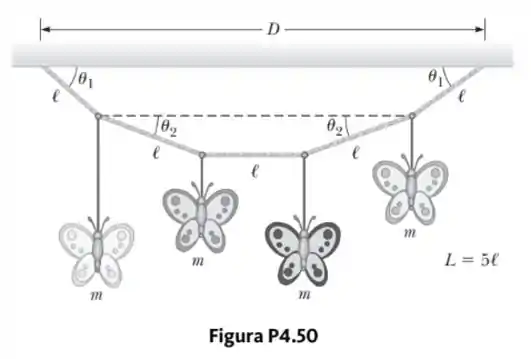
Um móbile é formado por quatro borboletas de metal de massa m sustentadas por uma corda de comprimento L . Os pontos de suporte são espaçados à mesma distância l , como mostrado na Figura P4.50. A corda forma um ângulo θ 1 com o teto em cada ponta. A seção central da corda é horizontal.

  1. Encontre a tensão em cada seção de corda em termos de θ 1 , m e g .
  2. Em termos de θ 1 , encontre o ângulo θ 2 que as seções de corda entre as borboletas de fora e as borboletas de dentro formam com a horizontal.
  3. Mostre que a distância D entre as extremidades da corda é

D = L 5 2 cos ⁡ θ 1 + 2 c o s ⁡ t g - 1 1 2 t g   θ 1 + 1

Passo 1

E aiii galera,

Vamos fazer mais uma questão?

Bora lá!

Abaixo, temos o esquema de forças:

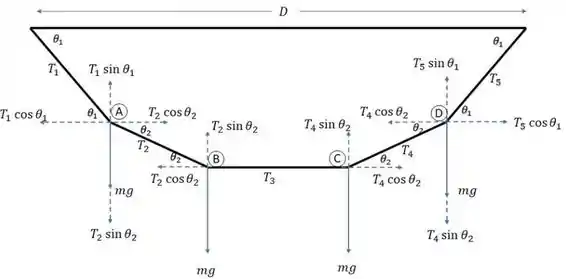
Passo 2

Letra a:

No ponto A:

∑ F x = T 2 cos ⁡ θ 2 - T 1 cos ⁡ θ 1 = 0 T 2 cos ⁡ θ 2 = T 1 cos ⁡ θ 1         ( 1 ) ∑ F y = T 1 sin ⁡ θ 1 - m g - T 2 sin ⁡ θ 2 = 0 T 1 sin ⁡ θ 1 = m g + T 2 sin ⁡ θ 2         ( 2 )

No ponto B:

∑ F x = T 3 - T 2 cos ⁡ θ 2 = 0 T 3 = T 2 cos ⁡ θ 2         ( 3 ) ∑ F y = T 2 sin ⁡ θ 2 - m g = 0 T 2 sin ⁡ θ 2 = m g           ( 4 )

No ponto C:

∑ F x = T 4 cos ⁡ θ 2 - T 3 = 0 T 3 = T 4 cos ⁡ θ 2         ( 5 ) ∑ F y = T 4 sin ⁡ θ 2 - m g = 0 T 4 sin ⁡ θ 2 = m g           ( 6 )

No ponto D:

∑ F x = T 5 cos ⁡ θ 1 - T 4 cos ⁡ θ 2 = 0 T 5 cos ⁡ θ 1 = T 4 cos ⁡ θ 2       ( 7 )

∑ F y = T 5 sin ⁡ θ 1 - m g - T 4 sin ⁡ θ 2 = 0 T 5 sin ⁡ θ 1 = m g + T 4 sin ⁡ θ 2   ( 8 )

Passo 3

Comparando (4) com (6), então T 2 = T 4 . E vemos que T 5 = T 1 .

Então,

T 3 = T 1 cos ⁡ θ 1

T 1 sin ⁡ θ 1 = m g + m g T 1 sin ⁡ θ 1 = 2 m g

2 m g T 3 = t a n ⁡ θ 1 T 3 = 2 m g tan ⁡ θ 1

2 m g tan ⁡ θ 1 = T 1 cos ⁡ θ 1 T 1 = 2 m g sin ⁡ θ 1

Passo 4

Como,

tan ⁡ θ 2 = m g T 1 cos ⁡ θ 1

Substituindo T 1 em (12):

tan ⁡ θ 2 = m g 2 m g sin ⁡ θ 1 cos ⁡ θ 1 = tan ⁡ θ 1 2 θ 2 = tan - 1 ⁡ 0.5 tan ⁡ θ 1

Substituindo θ 2 em (4):

T 2 sin ⁡ tan - 1 ⁡ 0.5 tan ⁡ θ 1 = m g

T 2 = m g sin ⁡ tan - 1 ⁡ 0.5 tan ⁡ θ 1

Passo 5

Letra b:

tan ⁡ θ 2 = m g 2 m g sin ⁡ θ 1 cos ⁡ θ 1 = tan ⁡ θ 1 2 θ 2 = tan - 1 ⁡ 0.5 tan ⁡ θ 1

Passo 6

Letra c:

Podemos ver, do diagrama, que D iguala os componentes x de todos os segmentos da corda e sabemos que L = 5 l , então nós temos:

D = l c o s ⁡ θ 1 + l c o s ⁡ θ 2 + l + l c o s ⁡ θ 2 + l c o s ⁡ θ 1 = 2 l c o s ⁡ θ 1 + 2 l c o s ⁡ θ 2 + t = l 2 l c o s ⁡ θ 1 + 2 l c o s ⁡ θ 2

D = L 5 2 l cos ⁡ θ 1 + 2 l cos ⁡ tan - 1 ⁡ 0.5 tan ⁡ θ 1

Resposta

  1. T 1 = 2 m g sin ⁡ θ 1 , T 2 = m g sin ⁡ tan - 1 ⁡ 0.5 tan ⁡ θ 1 , T 3 = 2 m g tan ⁡ θ 1
  2. θ 2 = tan - 1 ⁡ 0.5 tan ⁡ θ 1
  3. Ver resolução
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois blocos idênticos estão ligados por um cordão sem massa que passa por uma polia, como mostrado na figura abaixo. Inicialmente, o ponto do meio do cordão está passando pela polia e a superfície sob
Um bloco de massa m 1 está sobre uma mesa horizontal. O bloco está preso a um bloco de 2,5k g ( m 2 ) através de um fio leve que passa por uma polia, sem massa e sem atrito, na beirada da mesa. O bloc
Na figura 4-38a, um bloco de 0,500 kg está suspenso pelo ponto central de um fio de 1,25 m. As extremidades do fio estão presas ao teto em pontos separados de 1,00 m. (a) Qual é o ângulo que o fio for
Duas bolas idênticas de 15,0k g , e 25,0c m de diâmetro cada uma, estão suspensas por dois fios de 35,0c m , como indicado na Figura 5.67 . Todo o aparato é suportado por um único fio de 18,0c m e as
O bloco de 4,0k g da Figura 5.78 está preso a um eixo vertical por meio de dois fios. Quando o sistema gira em torno desse eixo, os fios ficam dispostos como indicado no diagrama e a tensão no fio sup