Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 18
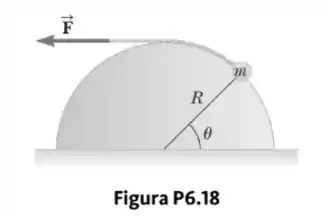
Uma partícula pequena de massa é puxada para a parte superior de um meio-cilindro sem atrito (de raio ) por uma corda leve que passa sobre o topo do cilindro, como mostrado na Figura P6.18.
- Considerando que a partícula se move a uma velocidade escalar constante, mostre que . Observação: Se a partícula se move a uma velocidade escalar constante, a componente de sua aceleração tangente ao cilindro deve ser zero todas as vezes.
- Integrando diretamente , encontre o trabalho realizado para mover a partícula, a velocidade escalar constante da parte inferior à parte superior do meio-cilindro.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Letra a:
O raio do objeto faz ângulo com a horizontal. Tomando o eixo x na direção do movimento tangente ao cilindro, o peso do objeto faz um ângulo com o eixo - x. Então:
Passo 2
Letra b:
Usamos a medida em radianos para expressar o próximo deslocamento como em termos do próximo ângulo movido:
Resposta
Exercícios de Livros Relacionados
A Fig. 7-39 mostra a aceleração de uma partícula de 2,00k g sob a ação de uma força F que desloca a partícula ao longo de um eixo x , a partir do repouso, de x=0 a x=9,0m . A escala vertical do gráfic
A Fig. 7-40 mostra uma corda presa a um carrinho que pode deslizar sobre um trilho horizontal sem atrito ao longo de um eixo x . A extremidade esquerda da corda é puxada através de uma polia de massa
Um bloco de 1,5k g está em repouso sobre uma superfície horizontal sem atrito quando uma força ao longo de um eixo x é aplicada ao bloco. A força é dada por F x =2,5 - x 2 i →N , onde x está em metros
Uma força F=c x -3,00 x 2 i → , onde F está em newtons, x em metros e e é uma constante, age sobre uma partícula que se desloca ao longo de um eixo x . Em x= 0 , a energia cinética da partícula é 20,0
A força a que uma partícula está submetida aponta ao longo de um eixo x e é dada por F = F 0 ( x / x 0 - 1 ). Determine o trabalho realizado pela força ao mover a partícula de x= 0 a x=2 x 0 de duas f