Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 71
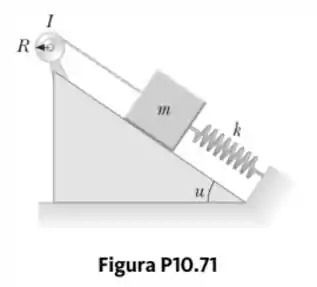
Se a polia mostrada na Figura P10.71 tem raio e momento de inércia . Uma ponta do bloco de massa é conectada a uma mola de constante força , e a outra é presa a uma corda ao redor do carretel. O eixo dele e a rampa não têm atrito. A polia é enrolada em sentido anti-horário de modo que a mola se estica por uma distância de sua posição encolhida, e ele é, então, solto do repouso. Encontre a velocidade angular do carretel quando a mola é esticada novamente.
Passo 1
E aiii gente, tudo bem com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo!
O bloco e o final da mola são puxados a uma distância d até a inclinação e depois soltos. A velocidade angular da bobina e a velocidade do bloco são relacionados por . O sistema está isolado, então:
Resposta
Exercícios de Livros Relacionados
Partindo simultaneamente do repouso, uma moeda e uma argola rolam sem deslizar, descendo um plano inclinado. Qual das seguintes afirmativas é verdadeira? (a) A argola chega primeiro embaixo. (b) A moe
Uma roda, partindo do repouso, gira com aceleração angular constante de 2,6r a d / s 2 . Após 6,0s da partida: (a) Qual é sua rapidez angular? (b) Qual é o ângulo varrido pela roda? (c) Quantas voltas
Uma bola de beisebol é atirada a 88m i / h e girando em torno de si a 1500r e v / m i n . Se a distância entre o lançador e a luva do pegador é cerca de 61p é s é , estime quantas revoluções a bola fa
Uma partícula se move com uma rapidez constante de 25m / s em um círculo de 90m de raio. (a) Qual é a sua rapidez angular em radianos por segundo em relação ao centro do círculo? (b) Quantas voltas el
Uma bicicleta de 14k g tem rodas de 1,2m de diâmetro, cada uma com uma massa de 3,0k g . A massa do ciclista é 38k g . Estime a fração da energia total do sistema ciclista-bicicleta que está associada