Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 66

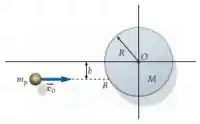
Um projétil de massa m p está se deslocando, com velocidade constante v → 0 , de encontro a um disco estacionário de massa M e raio R que é livre para girar em torno de seu eixo (Figura 10-54). Antes do impacto, o projétil está viajando ao longo de uma linha afastada de uma distância b abaixo do eixo. O projétil atinge o disco e gruda no ponto B . Use o modelo de massa pontual para o projétil. (a) Antes do impacto, qual é a quantidade de movimento angular total L 0 do sistema disco-projétil em relação ao eixo? Responda às seguintes questões em termos dos símbolos fornecidos no início do problema. (b) Qual é a rapidez angular ω do sistema disco-projétil logo após o impacto? (c) Qual é a energia cinética do sistema disco-projétil após o impacto? (d) Quanta energia mecânica é perdida nesta colisão?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como o torque externo resultante que age no sistema é nulo, sabemos que a quantidade de movimento angular é conservada em uma colisão perfeitamente inelástica. Portanto:

L 0 = m p v 0 b

Passo 2

O item (b) nos pede a velocidade angular após o impacto:

L 0 = I ω

ω = L 0 I

O momento de inércia, a partir do teorema dos eixos paralelos, é dado por:

I = 1 2 M R 2 + m p R 2

I = 1 2 R 2 M + 2 m p

Portanto:

ω = m p v 0 b 1 2 R 2 M + 2 m p

ω = 2 m p v 0 b R 2 M + 2 m p

Passo 3

O item (c) nos pede a energia cinética após o impacto:

K f = L 2 2 I = m p v 0 b 2 2 1 2 R 2 M + 2 m p

K f = m p v 0 b 2 R 2 M + 2 m p

Passo 4

Item (d):

A diferença entre a energia cinética inicial e a energia cinética final é dada por:

∆ E = K i - K f

∆ E = 1 2 m p v 0 2 - m p v 0 b 2 R 2 M + 2 m p

∆ E = 1 2 m p v 0 2 1 - 2 m p b 2 R 2 M + 2 m p

Resposta

a )   L 0 = m p v 0 b

b ) ω = 2 m p v 0 b R 2 M + 2 m p

c ) K f = m p v 0 b 2 R 2 M + 2 m p

d )   ∆ E = 1 2 m p v 0 2 1 - 2 m p b 2 R 2 M + 2 m p

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra homogênea (de 0,60m de comprimento e 1,0k g de massa) da Fig. 11-54 gira no plano do papel em torno de um eixo que passa por uma das extremidades, com um momento de inércia de 0,12k g ∙ m 2 .
Na Fig. 11-56, uma criança de 30k g está em pé na borda de um carrossel estacionário de raio 2,0m . O momento de inércia do carrossel em relação ao eixo de rotação é 150k g ∙ m 2 . A criança agarra um
Um disco uniforme de massa 10 m e raio 3,0 r pode girar livremente como um carrossel em torno do centro fixo. Um disco homogêneo menor de massa m e raio r está sobre o disco maior, concêntrico com ele
Um trapezista pretende dar quatro cambalhotas em um intervalo de tempo ∆ t = 1,87s antes de chegar ao companheiro de número. No primeiro e no ultimo quarto de volta,mantem o corpo esticado como na Fig
Na Fig. 11-53, uma bala de 1,0g é disparada contra um bloco de 0,50k g preso à extremidade de uma barra não homogênea de 0,50k g com 0,60m de comprimento. O sistema bloco-barra-bala passa a girar no p