Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 52

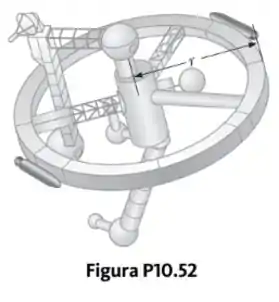
Uma estação espacial é construída no formato de um anel oco de massa 5,00 × 10 4   k g . Os membros da equipe caminham por um deque formado pela superfície interna da parede cilíndrica externa do anel, com raio r   =   100   m . No repouso, quando construído, o anel foi colocado em rotação em torno do seu eixo de modo que as pessoas dentro experimentassem uma aceleração de queda livre efetiva igual a g . (Ver Fig. P10.52.) A rotação é atingida ao disparar dois pequenos foguetes presos tangencialmente aos pontos opostos sobre a borda do anel.

  1. Que momento angular a estação especial adquire?
  2. Por qual intervalo de tempo os foguetes devem ser disparados se cada um exerce um impulso de 125   N ?

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Nós queremos:

a c = g = v 2 r = ω 2 r

Então,

ω = g r = 9.80 m s 2 100 m = 0.313 r a d / s I = M r 2 = 5 × 10 4 k g ( 100 m ) 2 = 5 × 10 8 k g ⋅ m 2

Passo 2

Letra a:

L = I ω = 5 × 10 8 k g ⋅ m 2 0.313 r a d s = 1.57 × 10 8 k g ⋅ m 2 s

Passo 3

Letra b:

Δ t = L f - 0 ∑ τ = 1.57 × 10 8 k g ⋅ m 2 s 2 125 N 100 m = 6.26 × 10 3 s = 1.74 h

Resposta

  1. 1.57 × 10 8 k g ⋅ m 2 s
  2. 1.74 h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois astronautas (Fig. P10.67), cada um com massa M , estão conectados por uma corda de comprimento d de massa desprezível. Eles estão isolados no espaço, orbitando seu centro de massa com velocidade
10.2Q Por que um carro levanta sua frente durante a arrancada e a abaixa durante a freada? Isso acontece com qualquer carro?
9.4Q Suponha que a Lua no passado tenha tido velocidade angular de rotação em torno do seu eixo diferente de sua velocidade angular orbital. As marés causadas pela Terra sobre a Lua seriam então muito
9.10P O disco visto na Figura 9.18 gira com velocidade ω 0 em torno do eixo vertical de simetria. Uma lança, caindo na vertical, crava-se à distância a do eixo e rotação. Para quanto cai a velocidade
Conforme discutimos na Seção 10.6, o momento angular de uma acrobata no circo se conserva à medida que ela se move pelo ar. Seu momento linear se conserva? Explique sua resposta.