Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 41
Um vetor tem um componente de unidades e um componente de unidades. Encontre o módulo e a direção e o sentido desse vetor.
Passo 1
Para encontrarmos o módulo do vetor , teremos que utilizar a seguinte equação.
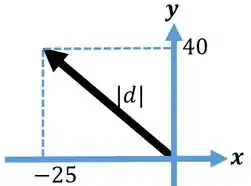
Onde é a será o módulo. Substituindo temos.
O módulo do vetor é , da direita para esquerda de baixo para cima.
Resposta
O módulo do vetor é 47,17, da direita para esquerda de baixo para cima.
Exercícios de Livros Relacionados
O vetor A→ está situado no plano x y . Ambas as componentes serão negativas se o vetor apontar da origem para dentro de qual quadrante? do primeirodo segundodo terceirodo quarto quadrantedo segundo ou
Um vetor aponta da origem para dentro do segundo quadrante do plano x y . O que você pode concluir sobre seus componentes? Ambas as componentes são positivasA componente x é positiva e y , negativaA c
Uma mosca pousa na parede de um quarto. O canto inferior esquerdo da parede é selecionado como a origem de um sistema de coordenadas cartesianas bidimensional. Se a mosca estiver localizada no ponto c
Dois pontos no plano x y têm coordenadas cartesianas ( 2,00 ,– 4,00 )m e ( – 3,00 ,3,00 )m . Determine:a) a distância entre esses pontosb) suas coordenadas polares
O vetor B → tem componentes x , y e z de 4,00 , 6,00 e 3,00 unidades, respectivamente. Calcule a) o módulo de B → b) o ângulo que B → forma com cada eixo de coordenadas