Lei de Ampère
Teoria
Fala aí, nós somos o Responde Aí, e nossa missão hoje é te mostrar a Lei de Ampère!
O que diz a Lei de Ampère?
Quando uma corrente percorre um fio condutor, ela gera um campo magnético. Assim:
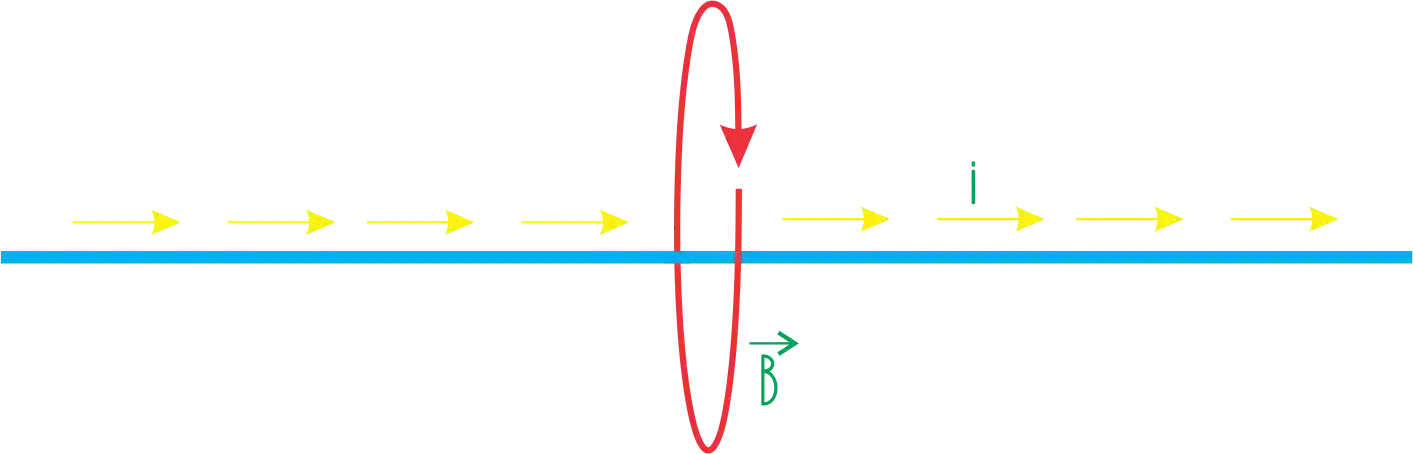
É ai que entra a lei de Ampère! Ela serve para calcular o campo magnético ao redor de um fio condutor onde passa corrente.
A fórmula da Lei de Ampère tem essa carinha aqui:
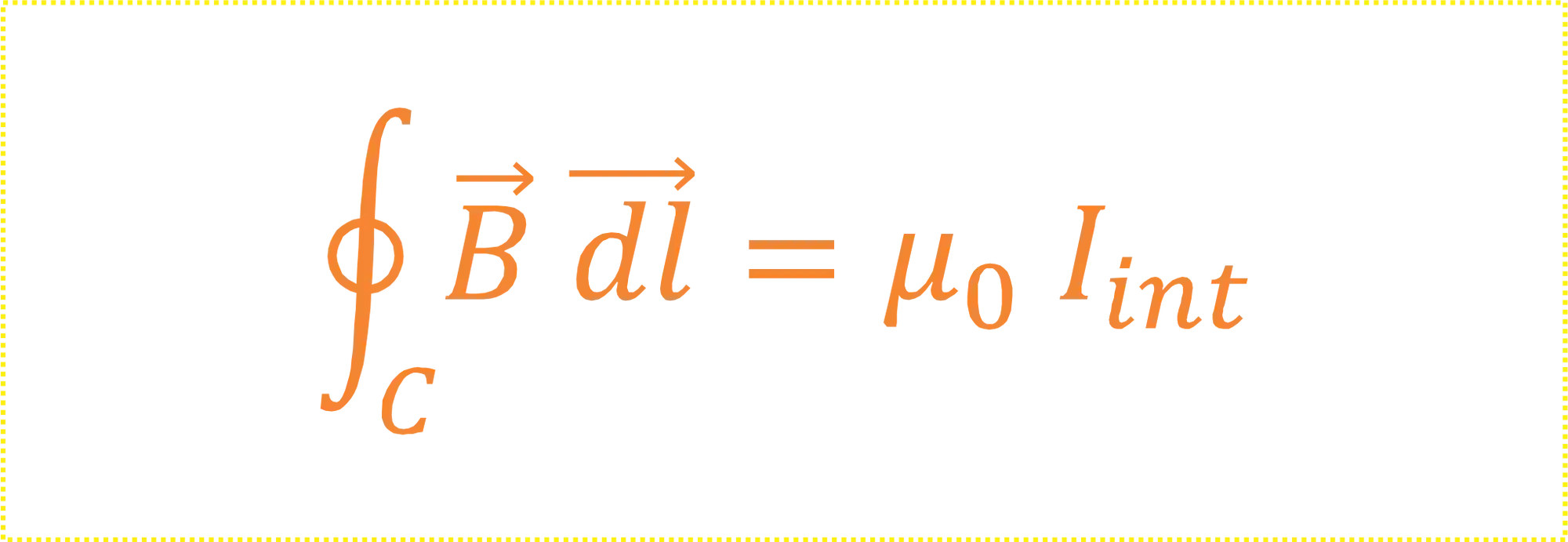
Mas calma, não se assusta! A gente vai entender tudinho sobre a lei de Ampère! Vamos começar dando nome aos bois 🐮:
é uma curva fechada, que chamamos de curva amperiana. Ela é essa curva vermelha com uma setinha que vimos na imagem lá do início! - O vetor
é o vetor infinitesimal do comprimento da curva, ele é tangente a em todos os pontos; é o vetor campo magnético, sobre a curva ; é a permeabilidade magnética no vácuo; é a corrente elétrica constante que passa por dentro da curva .
Ainda tá preocupado com como você vai usar essa fórmula esquisitona?! E se eu te contasse que a gente vai simplificar ela!?
A lei de Ampère simplificada fica assim:
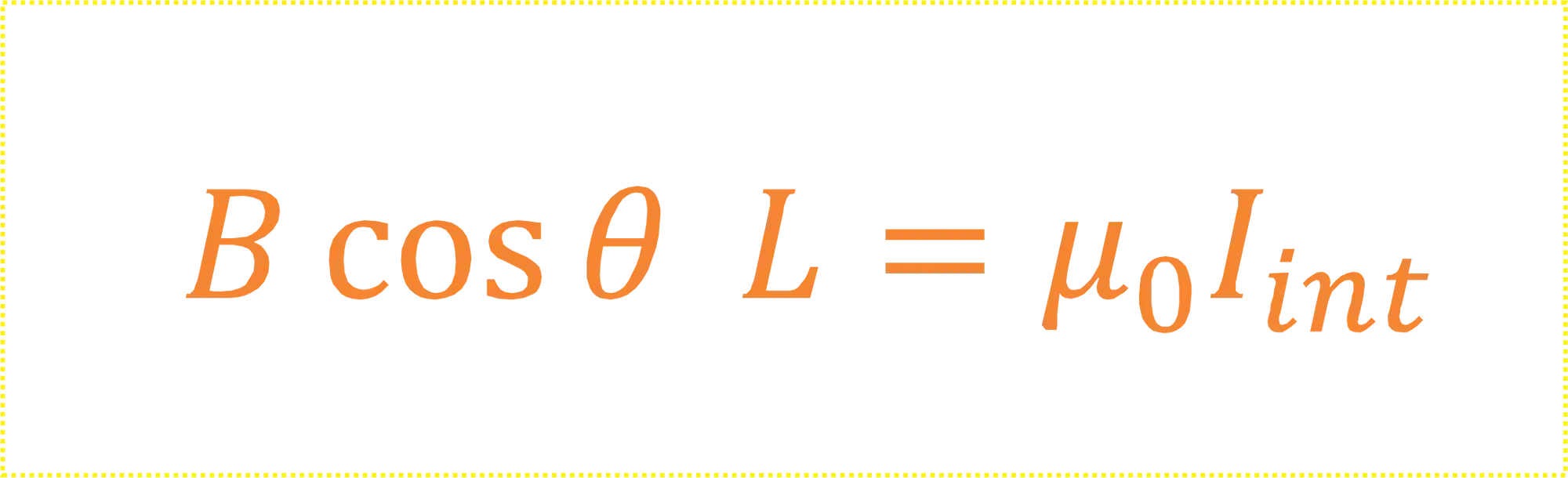
Só que pra a gente sair da lei de Ampère lá de cima e chegar nessa forma mais simpática, temos que ter em mente algumas considerações pra a gente não usar ela da forma errada!
Nesse vídeo abaixo a gente te explica que considerações são essas e muito mais, se liga só 👇
📢 Clique para ver mais:
Lei de Ampère: Hipóteses
Como a gente falou lá em cima, pra chegarmos na versão simplificada da lei de Ampère, temos que lançar mão de algumas considerações!
Então bora lá entender que considerações são essas. Se liga nessa imagem, que vai ficar mais claro:
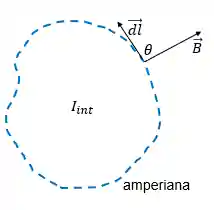
Imagina que o fio condutor esta entrando (ou saindo) da tela com a corrente elétrica! Essa curva amperiana é nossa curva imaginária onde vamos calcular a integral de linha.
Dentro da integral nós temos um produto escalar entre dois vetores, então, podemos reescrever esse produto em função do módulo dos vetores e do cosseno do ângulo que se forma entre eles:
Se o campo sobre a curva
A integral de
Assim, ficamos com uma expressão muito mais simples, não é mesmo? Mas é necessário a gente se atentar para as simplificações que OBRIGATORIAMENTE precisam estar presentes para que a Lei de Ampère fique mais simples assim:
- O módulo do campo magnético tem que ser constante em todo o comprimento da curva, só assim podemos tirá-lo da integral.
- Além do módulo de campo magnético constante, também precisamos que o ângulo que ele faz com o vetor unitário de comprimento da curva
também seja constante, para assim tirar o cosseno da integral.
- A curva amperiana não precisa necessariamente ser circular, ela pode ter qualquer formato estranho, mas lembra que nessa forma simplificada nós temos que achar o comprimento da curva, então é bom tentarmos supor uma amperiana tendo um formato conhecido!
Topa fazer um exercício aqui comigo para ver na prática como funciona a lei de ampère? Então bora!
Exercício: Calcule o módulo do campo magnético,
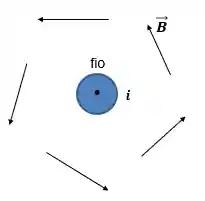
A questão já nos mostra o vetor campo magnético gerado pela corrente e quer saber só o módulo, então vamos usar a forma já simplificada, lembrando das considerações que precisam ser respeitadas, beleza?
Vamos escolher uma amperiana circular e que tem o centro coincidindo com o centro do fio. O módulo do campo magnético depende da distância em relação a corrente que o está gerando, se a amperiana é circular e é concêntrica com o fio todos os pontos da amperiana estão a mesma distância do fio e assim garantimos que o módulo do campo seja igual em todos os pontos da amperiana:
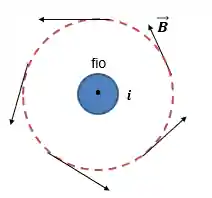
Vamos colocar o vetor
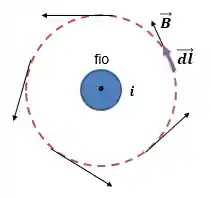
Assim garantimos que o ângulo entre o vetor campo magnético e o vetor comprimento seja sempre zero.
Agora, podemos aplicar a fórmula:
O comprimento da curva podemos calcular rapidamente como sendo o comprimento da circunferência:
E o cosseno de zero nós sabemos:
E a corrente elétrica interna é a corrente
Agora, podemos substituir na equação e encontrar o módulo do campo magnético em função de
Prontinho!!
Regra da Mão direita
A regra da mão direita nos ajuda a definir o sentido do campo magnético formado!
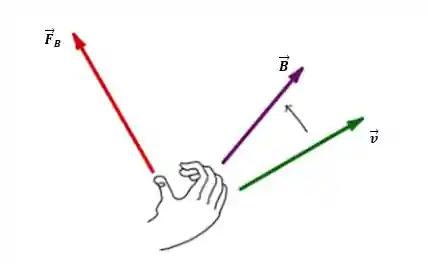
Aqui não tem mistério! Devemos fazer o seguinte: os 4 dedos, com exceção do polegar, apontam na direção do vetor
Agora, se você ainda tiver dúvidas, se liga nesse vídeozinho que o Responde Aí preparou pra você sobre Lei de Ampère:
Agora vamos praticar com exercícios?
Regra da Mão direita
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – Prova Final – 2014.2 – Múltipla Escolha nº4
Considere as seguintes afirmações:
- O campo magnético de uma espira circular por onde passa uma corrente estacionária satisfaz a lei de Ampère.
- A afirmação é verdadeira devido à simetria axial da espira.
- Se a espira fosse quadrada, a lei de Ampère não seria válida.
- Se a espira fosse quadrada, a lei de Ampère seria válida, desde que se escolhessem curvas amperiana que passassem pelo centro do quadrado.
São verdadeiras as afirmativas:
Somente
e
, e
e
Somente
Passo 1
Vamos analisar uma afirmativa por vez, ok?
- O campo magnético de uma espira circular por onde passa uma corrente estacionária satisfaz a lei de Ampère.
A lei de Ampère é dada por:
Assim, é possível aplicar a lei de Ampère a este caso.
A afirmação é verdadeira.
Passo 2
- A afirmação é verdadeira devido à simetria axial da espira.
A simetria pode facilitar os cálculos, mas não é um requisito para aplicar a lei de Ampère.
A afirmação é falsa.
Passo 3
- Se a espira fosse quadrada, a lei de Ampère não seria válida.
Novamente, a simetria não é um requisito para aplicar a lei de Ampère. Dessa forma, a lei permaneceria válida se a espira fosse quadrada.
A afirmação é falsa.
Passo 4
- Se a espira fosse quadrada, a lei de Ampère seria válida, desde que se escolhessem curvas amperiana que passassem pelo centro do quadrado.
A única exigência da lei de Ampère é que a amperiana envolva todas as correntes.
Logo, a afirmativa é falsa.
A opção correta é a letra .
Resposta
Somente
Exercício Resolvido #2
UFRJ – Prova 2 – 2014.2 – Múltipla Escolha nº4
Seja uma superfície esférica S, dividida em duas metades e por um grande círculo . A partir da lei de Ampère, podemos afirmar que:
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A circulação do campo magnético ao longo de é nula.
Passo 1
Vamos analisar uma alternativa de cada vez, ok?
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A lei de Ampère não trabalha com o fluxo de campo magnético, apenas com a circulação de . Logo, essa aqui é falsa.
Passo 2
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
A lei de Ampère diz que a circulação do campo magnético ao longo de é proporcional à intensidade de corrente que atravessa a curva , então seria proporcional à intensidade da corrente através de uma das metades da esfera ou .
Passo 3
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
Acabamos de falar nisso, essa afirmativa é correta.
Passo 4
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
Novamente, a lei de Ampère nem menciona “fluxo de campo magnético”, essa afirmativa é falsa.
Passo 5
A circulação do campo magnético ao longo de é nula.
A circulação só seria nula se a corrente englobada pela curva fosse nula.
A afirmativa é falsa.
Resposta
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
Exercício Resolvido #3
UFRJ – Prova 2 – 2013.1 – Múltipla Escolha nº5.
Determine a circulação para as três curvas fechadas orientadas respectivamente.
- pois todas são perpendiculares.
Passo 1
Clássica questão de circulação de corrente. Pela regra da mão direita, colocamos nossos dedos alinhados à orientação de cada curva e determinamos os sentidos dos vetores área.
À partir daí sabemos qual corrente é positiva e qual é negativa. Fazendo um por um:
Esse último tem aquela sacanagem de dividir em duas curvas:
Portanto temos nossa resposta.
Resposta
Letra e
Exercício Resolvido #4
UFRJ – Prova 2 – 2014.1 – Múltipla Escolha nº2.
A figura a seguir mostra a seção reta de três fios que conduzem correntes estacionárias, com intensidade de mesmo módulo , que atravessam o plano da figura com sentidos indicados na mesma.
Quatro curvas orientadas indicadas pelas letras até são apresentadas na figura. A alternativa a seguir que melhor relaciona a circulação do campo magnético em cada curva é
.
.
.
.
.
Passo 1
Quando o problema pede para calcularmos a circulação , no fundo, ele tá implorando pra usarmos a lei de Ampère, dada por:
Ou seja, para cada curva, o nosso único trabalho é calcular a corrente interna englobada pela amperiana.
O que vai determinar se vamos considerar a corrente positiva ou negativa vai ser o sentido da orientação da curva.
Se a curva estiver orientada no sentido anti-horário, as corrente que estiverem saindo da página serão positivas, e as correntes que estiverem entrando na página serão negativas.
Se a curva estiver orientada no sentido horário, as corrente que estiverem entrando na página serão positivas, e as correntes que estiverem saindo da página serão negativas.
Ok, vamos nessa!
Passo 2
A curva não possui nenhuma corrente, logo:
A curva possui uma corrente entrando na página, como ela está orientada no sentido anti-horário:
A curva possui uma corrente entrando e uma saindo, logo:
A curva está orientada no sentido anti-horário e possui 2 correntes saindo e uma entrando, logo:
Assim, a opção correta é a letra .
Resposta
.
Exercício Resolvido #5
PUCRIO – Prova 2 – 2014.2 – Questão 3.
Um fio cilíndrico de raio transporta uma corrente uniformemente distribuída por sua seção reta e com sentido saindo do papel.
Encontre os raios das espiras amperianas circulares centradas no eixo do fio para as quais o campo magnético gerado pelo fio é dado por:
Passo 1
Para determinar os raios das amperianas, precisamos usar a lei de Ampère, que diz o seguinte:
Nossa curva será um círculo. Pela simetria, temos que o campo magnético (dado pela regra da mão direita) será sempre paralelo ao vetor , e será sempre constante. Temos, então:
Passo 2
Vamos começar calculando o raio !
Para esse raio, a corrente interna não vai ser a corrente total.
Como a corrente é uniformemente distribuída, temos que a corrente por unidade de área é constante, então se liga!
Para , a corrente interna à amperiana fica:
Agora é só substituir os valores na Lei de Ampére e correr para o abraço!
Belezinha! Para determinar , fica mais fácil ainda porque a corrente interna é dada, . Vamos pro próximo passo!
Passo 3
Para esse raio, a corrente interna será . Substituindo os valores na Lei de Ampère, temos:
Resposta
;
Exercício Resolvido #6
UFRJ – Prova 2 – 2014.2 – Múltipla Escolha nº3.
Por um condutor cilíndrico maciço e infinito de raio passa uma corrente estacionária e axial uniformemente distribuída através de sua seção reta. O campo magnético a uma distância radial do eixo do condutor, em coordenadas cilíndricas , é igual a
e .
e .
e .
e .
e .
Passo 1
O sentido do campo magnético é determinado através da regra da mão direita. Assim, o campo terá direção tangencial e não radial .
Então já poderíamos eliminar as opções e .
Beleza, agora vamos calcular esses caras!
O módulo do campo magnético é determinado através da lei de Ampère, dada por:
Por conta da simetria do problema, a nossa amperiana será uma circunferência de raio , sendo assim:
Se preferir, como já sabemos a direção e sentido desse cara, podemos já colocá-lo na forma de vetor:
Então, o nosso trabalho vai ser apenas calcular a corrente para cada região.
Passo 2
- :
- :
Essa região está no interior do fio. Como sabemos que a corrente é distribuída uniformemente através de sua seção reta, para calcularmos a corrente interna, basta fazer uma regra de 3:
Substituindo na expressão de , teremos:
Passo 3
Como essa corresponde à região externa ao fio, , logo:
A resposta certa é a letra .
Resposta
e .
Exercício Resolvido #7
PUCRIO – Prova 2 – 2015.1 – Questão 3.
Considere o cabo coaxial muito longo da figura ao lado, formado por duas cascas cilíndricas concêntricas com raios internos , e raios externos , , respectivamente. Uma corrente uniforme flui na casca cilíndrica interna com o sentido para fora do plano do papel e uma corrente uniforme com sentido desconhecido flui na casca cilíndrica externa.
Calcule a intensidade do campo magnético nas regiões:
;
;
;
Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.
Calcule a amplitude do campo magnético em em função da corrente .
Passo 1
;
Esse é um problema clássico de Lei de Ampère, dada por:
Podemos dar uma simplificada na expressão acima:
Onde a integral será igual ao comprimento da nossa amperiana que, nesse caso, será uma circunferência de raio :
Assim, para cada caso, o nosso único trabalho é calcular a corrente englobada pela amperiana.
A amperiana de raio não engloba nenhuma corrente, logo:
Passo 2
;
A amperiana com esse raio engloba apenas parte da primeira casca cilíndrica.
Como a corrente é uniformemente distribuída pela sessão transversal da casca cilíndrica, podemos determinar com uma regra de 3:
Substituindo na expressão do campo magnético, teremos:
Passo 3
;
A amperiana com esse raio engloba toda a primeira casca cilíndrica, logo:
Logo:
Passo 4
Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.
Vamos usar a Lei de Ampère para calcular o campo magnético a uma distância do centro.
Novamente, o campo magnético terá essa cara:
Esse campo magnético deve ser igual ao campo dado pelo enunciado, logo:
Simplificando:
Isso significa que a corrente está se somando à corrente e, por isso, o seu sentido também é para fora do papel.
Agora, o nosso trabalho é calcular a corrente englobada pela amperiana de raio .
Passo 5
A amperiana vai englobar toda a casca cilíndrica de corrente e parte da casca cilíndrica externa.
Logo:
Pra determinar , vamos fazer o mesmo que fizemos anteriormente, calculando através de uma regra de 3:
Portanto:
Voltando ao problema:
Finalmente:
Passo 6
Calcule a amplitude do campo magnético em em função da corrente .
Esse raio engloba as duas cascas cilíndricas, logo:
Assim, o campo magnético será dado por:
Resposta
Exercício Resolvido #8
UFRJ – Prova 2 – 2013.1 – Questão discursiva 1.
Um cabo coaxial é composto por um fio sólido, cilíndrico, circular, de raio , e uma casca espessa, cilíndrica, também circular, coaxial, de raios e , tais que . Ambos os cilindros são muito longos. Através do fio interno, passa uma corrente elétrica, estacionária, cuja densidade de corrente é , enquanto que, através da casca externa, passa uma corrente elétrica, também estacionária, com densidade de corrente .
- Qual é a (intensidade de) corrente elétrica no fio interno?
- Qual é a (intensidade de) corrente elétrica na casca externa?
- Determine o campo magnético em cada uma das quatro regiões típicas em que o cabo “divide” o espaço.
Passo 1
Sejam e as correntes nos fios interno e externo respectivamente. A intensidade de corrente elétrica pode ser calculada pela fórmula:
Onde é a seção reta do fio com uma certa orientação. Vamos estipular a orientação positiva, ou seja, o vetor área apontando no sentido de :
Fazendo o produto escalar para o fio interno:
Como é uma constante, sai fora da integral:
Integrando na seção reta do fio temos sua área:
Passo 2
Em seguida fazemos o mesmo para a casca externa:
Onde é a seção reta da casca cilíndrica externa. Temos que usar a mesma orientação da área de antes, senão nada faz sentido. O produto vetorial resulta:
Plugando na integral temos:
Integrando na casca cilíndrica externa obtemos sua área:
Passo 3
Vamos agora fazer um argumento genérico para todas as regiões de campo magnético e depois vamos só substituindo a corrente. Por se tratar de fios cilíndricos muito longos, temos uma simetria circular no campo magnético do problema.
Enunciando a Lei de Ampère:
Portanto escolhemos uma curva Amperiana circular de raio arbitrário . De forma que:
Em toda , o que implica:
Passo 4
Além disso temos que, pela configuração do campo, o módulo deste é constante em toda , portanto:
A integral de pedaços infinitesimais na Amperiana resulta no comprimento desta:
Como se trata de uma circunferência de raio , temos:
Como arbitramos tudo no sentido positivo de , basta multiplicar por para achar o sentido positivo do campo magnético. Quando a corrente for negativa ela já vai nos apontar o campo correto.
Agora a questão se resume a achar a corrente.
Passo 5
Na região , temos que a corrente interna é:
Onde nesse caso é o circulo de raio . Logo:
Logo o campo é:
Passo 6
Agora para a região temos que a única corrente é a do fio de raio que nós já tínhamos calculado na letra a, portanto:
Substituindo na equação de campo:
Passo 7
Para a região temos que a corrente interna tem contribuição tanto do fio de raio quanto da parte da casca que está dentro da Amperiana. Portanto:
Lembrando que a região entre e não tem corrente.
A corrente entre a casca externa e a Amperiana pode ser obtida pela integral (sério, até dá pra fazer sem a integral nesse caso pois é constante, mas se acostume a fazer com a integral que a chance de erro é bem menor):
Portanto a corrente interna é:
O campo então fica:
Passo 8
Por fim, a região pega somente a soma das correntes totais que tínhamos encontrado nas letras a e b:
Resposta
a)
b)
c)
Exercício Resolvido #9
Site do Prof. A. F. Guimarães, lista 05 de Física 9
Um fio retilíneo de raio conduz uma corrente constante . Um outro fio retilíneo de mesmo raio também conduz uma corrente constante , porém com sentido contrário ao da corrente que flui no primeiro fio. Estime o módulo do campo magnético para pontos externos aos dois fios, isto é, para distâncias (ao centro de um dos fios) maiores que . Suponha que os dois fio possuam uma fina camada de isolante e que eles estejam em contato lateral.
Passo 1
Vamos começar olhando para a representação da figura abaixo.
Tomando o contorno dado pela circunferência de raio igual a , teremos, de acordo com a lei de Ampère:
onde é a intensidade de corrente que passa por dentro do contorno.
Passo 2
Bem, como os dois condutores transportam correntes com a mesma intensidade, porém de sentidos contrários, a parte direita da equação aí de cima será nula. E isso significa que:
para o contorno escolhido. E o mesmo vale para contornos com raio acima de .
Resposta
Exercício Resolvido #10
Site do Prof. A. F. Guimarães, lista 09 de Física 3
Um cilindro comprido, com seu eixo orientado ao longo do eixo , possui uma densidade de corrente . A densidade de corrente, embora seja simétrica em relação ao eixo do cilindro, não é constante e varia de acordo com a relação:
para
, para
onde é o raio do cilindro, é a distância radial entre o ponto considerado e o eixo do cilindro e é uma constante dada em ampères.
(a) Mostre que é a corrente total que passa através da seção reta do fio.
(b) Usando a lei de Ampère, deduza uma expressão para o módulo do campo magnético na região .
(c) Obtenha uma expressão para a corrente contida em uma seção reta circular de raio e centralizada sobre o eixo do cilindro.
(d) Aplicando a lei de Ampère, deduza uma empressão para o módulo do campo magnético na região . Como se comparam os resultados dos itens (b) e (d) para ?
Passo 1
(a) Mostre que é a corrente total que passa através da seção reta do fio.
Para encontrar a corrente toal , temos que integrar a função densidade de corrente para toda a área da seção transversal . Assim, temos que:
onde . Assim sendo,
Passo 2
(b) Usando a lei de Ampère, deduza uma expressão para o módulo do campo magnético na região .
Utilizando a lei de Ampère:
onde é a corrente dentro da curva amperiana. Para os pontos externos ao condutor, podemos tomar uma circunferência como a nossa curva e integrar ao longo dela.
Como a corrente dentro da curva é a corrente total , temos que:
onde .
Passo 3
(c) Obtenha uma expressão para a corrente contida em uma seção reta circular de raio e centralizada sobre o eixo do cilindro.
Bem, para resolver esse item, podemos lembrar lá do que fizemos no item (a). Ali integramos a densidade de corrente de até o raio do cilindro . MAS, aqui queremos a corrente em uma seção reta circular de raio . Então, precisamos fazer a MESMA integral, mas com limites de até , sacou?
Com esse raciocínio, chegamos no valor de igual a:
Passo 4
(d) Aplicando a lei de Ampère, deduza uma empressão para o módulo do campo magnético na região . Como se comparam os resultados dos itens (b) e (d) para ?
Utilizando a lei de Ampère, temos que:
onde já estamos considerando a corrente interna como aquela calculada no item (c).
Logo,
Se fizermos na equação acima e no valor de encontrado no item (b), chegamos ao mesmo resultado:
Resposta
(b)
(c)
(d)