Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 74
74- Um condutor possui forma de um cilindro oco, sendo o raio interno e o raio externo. Ele conduz uma corrente uniformemente distribuída ao longo da sua seção reta. Deduza expressões para o módulo do campo magnético nas seguintes regiões:
Passo 1
O condutor tem a seguinte cara:
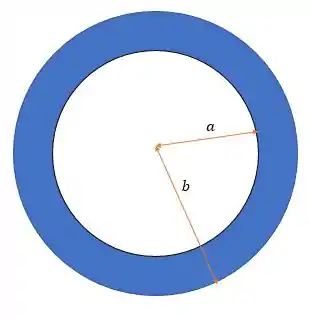
E como não temos nenhum corpo em então não haverá corrente passando por ele nesse intervalo, ou seja:
Passo 2
Já na área entre teremos uma corrente proporcional a área desse corpo (já que é uniformemente distribuída), ou seja quando e quando , então pela lei de Ampere temos:
Pois o comportamento da corrente depende exclusivamente da área formada por dentro da região cheia.
Ou seja quando teremos:
Passo 3
E quando teremos que a corrente será de (pois temos toda a área possível) então pela lei de Ampere teremos:
Que é o mesmo comportamento para quando a área é cheia, o que muda mesmo é o comportamento interno.