Potência em Circuitos de CA
Produzido por Bruno SoaresTeoria
Introdução
Bom você já deve ter calculado potência em circuitos de corrente contínua por aí, certo? Costumávamos usar:
Mas e se o circuito for diferente, e se tivermos uma fonte de corrente alternada nele? Tipo nesse camarada aqui:
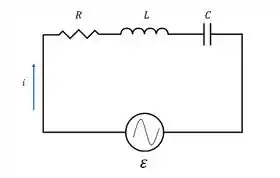
Se a reatância indutiva mede , a reatância capacitiva , a resistência do resistor é e a corrente é dada pela equação:
Como vamos calcular a potência?
Potência Real e Aparente
Em circuitos que são alimentados por um gerador de corrente alternada, a potência também vai variar com o tempo.
No geral ainda usaremos a equação usada em circuitos de corrente contínua pra calcular a potência, mas ela sofrerá algumas modificações.
A potência total do circuito, no caso do circuito RLC é chamada de potência aparente e é dada pela equação:
Onde é a voltagem da fonte, | é o módulo da impedância que funciona como a resistência equivalente e é a corrente máxima que é encontrada comparando a equação geral com a equação dada.
Mas por que chamamos de potência aparente?

Porque efetivamente só uma parte daquela potência vai gerar trabalho naquele circuito. É como uma caneca de cerveja onde a espuma só tá ali pra preencher o copo, saca só:
Então tá, mas e o que falta pra calcular essas duas potências e como eu calculo essa parte real?
A potência aparente depende da potência real, que é a parcela da potência dissipada pelo resistor e também é conhecida como potência ativa.
Onde e :
E também depende da parte não efetiva que é dissipada pelas reatâncias e é chamada de potência reativa.
A potência reativa é sempre a diferença em módulo entre as ddp dos capacitores do circuito e dos indutores multiplicada pela corrente.
Onde e :
E essa unidade aqui é nova, conhecida como Volt-Ampére reativo.
Enfim pra gente calcular a potência aparente temos que fazer uma soma vetorial entre as duas potências real e reativa.E aqui vai o pulo do gato pra trabalhar com potência: se a gente pegar o triângulo da impedância e multiplicar pela corrente máxima teremos o triângulo da potência que relaciona todas as potências que queremos calcular:
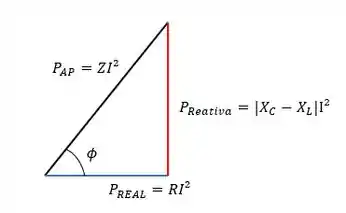
Podemos calcular a potência aparente a partir das outras duas potências, usando Pitágoras.
A unidade da potência aparente é Volt-Ampére.
E se você quiser ainda, calcular a impedância é só fazer:
Fator de Potência e Valores Médios
Bom não dá pra gente falar de potência e não falar do famoso fator de potência. Ele é a relação entre a potência real e potência aparente, e pode ser calculado como o cosseno do ângulo no triângulo das potências:
E com isso podemos calcular o fator de potência do nosso circuito:
Para maximizar a potência, deve-se manter o fator de potência o mais próximo de 1.
Bom chegamos até aqui sem olhar como fica a equação da potência com o tempo e realmente ela não é a mais importante e sim os módulos da potência de cada componente. Mas se você precisar apresentar a equação é só fazer:
Como não temos a voltagem, vale a pena usarmos a outra equação que depende da impedância:
Onde e , e enfim substituindo a equação fica:
Olhando essa equação da potência ao longo do tempo a gente pode observar que ela segue o padrão da corrente, temos um valor máximo multiplicando uma senóide mas nesse caso ao quadrado.
Sendo assim não é usual trabalharmos avaliando os valores de pico da potência. Para que possamos ter uma boa estimativa até de custos precisamos trabalhar com valores médios.
A potência que geralmente é avaliada numa rede é a potência média real. Ela depende da potência aparente média que é:
Onde e são os valores quadráticos médios da e da corrente, respectivamente dados por:
Enfim a gente pode usar de novo o triângulo da potência, ele também se aplica pra valores médios.
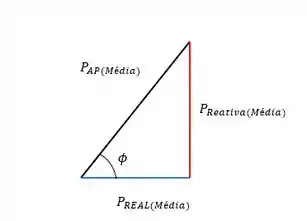
Daqui tiramos que:
Assim, a potência média é dada por:
Lembrando que:
E assim a potência média fica:
E a potência aparente que calculamos antes:
E o fator de potência calculado foi:
Sendo assim:
Transformadores
Também conhecido como transformadores de tensão, os transformadores são feitos com duas bobinas com números diferentes de enrolamento.
A tensão que vem da rede chega ao transformador na bobina primária que também é conhecida como núcleo primário. Essa tensão então é transformada e enviada a bobina secundária ou núcleo secundário.
A relação entre as tensões da bobina primária e secundária vai depender apenas do número de enrolamentos ou espiras de cada bobina.
Onde
é a tensão no transformador primário é a tensão no transformador secundário.
é o número de enrolamento da bobina primária e na secundária.
Nesse processo a energia se conserva então as potências também serão iguais:
Como:
Podemos encontrar até uma relação entre as correntes de cada bobina.
E para compararmos com o enrolamento é só deixar no modelo:
Então a relação da corrente com o número de enrolamentos fica:
O inverso da relação da voltagem.
