Fontes de CA e Reatância
Produzido por Bruno SoaresTeoria
Circuito de Carga Resistiva
A gente já conhece os circuitos comuns, e agora vamos conhecer um pouco sobre as fontes de corrente alternada. Vamos começar pelo circuito mais simples com um resistor e a fonte.
Nesse circuito temos um resistor e um gerador de corrente alternada.
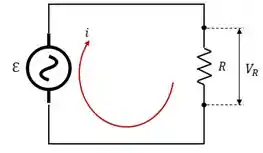
Como será que se comporta a corrente e a voltagem nesse circuito? O que será que essa fonte de corrente alternada vai trazer de diferente pra nós?
A fem é dada por:
Pela regra das malhas, temos que:
Onde é a diferença de potencial no resistor, dada por:
Para determinar a corrente, basta lembrar que , ou seja:
Onde é a amplitude da corrente na resistência, a constante de fase será nula para uma carga resistiva, logo:
Repara que a corrente é uma função seno multiplicada pela amplitude da corrente. A característica dessa função é oscilar no intervalo , e por causa dessa oscilação dizemos que a corrente é alternada.
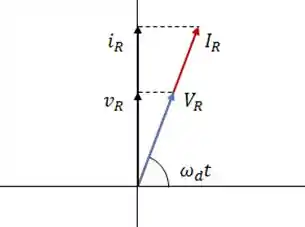
Podemos representar e geometricamente por fasores... calma, não é complicado! Os fasores e tem as seguintes propriedades:
- A velocidade angular com que ambos giram no sentido anti-horário é .
- O comprimento de cada fasor representa a amplitude, para temos e para temos .
- A projeção de cada fasor no eixo vertical representa o valor da grandeza para aquele .
Eles são representados assim:
Circuito de Carga Capacitiva
E como ficam os circuitos de carga capacitiva com corrente alternada? Se liga como ele é:
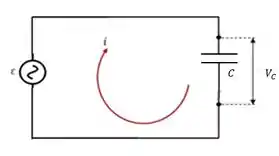
Onde a força eletromotriz vai ser dada por:
.
Utilizando o mesmo princípio de regra das malhas, temos que a variação do potencial no capacitor é
E para encontrarmos a corrente no capacitor, usamos a equação da corrente:
Substituindo a equação da voltagem dependente do tempo, temos:
Derivando e eliminando o termo semelhante , temos:
E aqui conheceremos um cara novo, que funciona como a resistência do capacitor e é conhecida como reatância capacitiva:
Guarde com carinho a equação da reatância, pra resolver alguns problemas você só precisa saber aplica-la e não necessariamente deduzi-la. Substituindo temos:
Precisamos deixar a corrente na mesma notação trigonométrica da voltagem, portanto vamos converter o cosseno em seno fazendo o seguinte:
Fazendo :
E podemos dizer que a amplitude da corrente é o que multiplica a função seno:
Então repara o seguinte, a corrente é adiantada de em relação a voltagem, vamos ver isso no diagrama fasorial?
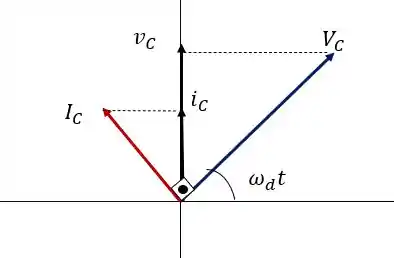
Geralmente nas provas e exercícios você vai ter um circuito com as componentes e a voltagem e vão te pedir pra calcular a função da corrente e esboçar ambos no diagrama fasorial, vamos praticar um pouco?
Vamos fazer o exemplo do circuito que vimos:
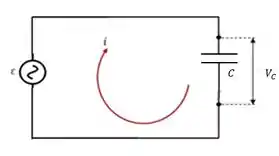
Onde a capacitância mede e a voltagem da fonte é dada pela equação:
Para isso calcular a voltagem máxima, a frequência do circuito, a reatância capacitiva e a corrente no capacitor. Após isso esboçar o diagrama fasorial.
Fazendo a lei das malhas do circuito temos o seguinte:
Da própria equação tiramos a voltagem máxima no capacitor que é a amplitude da função:
Mas e a frequência do circuito, como calcular? Bom é a frequência angular e a gente tira da equação também.
Tá, mas o exercício pediu a frequência e não a frequência angular!
Vamos chegar lá, é que precisamos dela pra calcular a frequência do circuito em
Beleza então vamos partir pra reatância capacitiva, lembra que:
Agora podemos partir pra corrente, lembrando que ela vai ser sempre adiantada em relação a voltagem de e sua amplitude é:
Então a função da corrente fica:
E pro diagrama de fasores não em mistério, é só lembrar que a corrente é adiantada de e representar isso colocando um ângulo de entre os vetores:
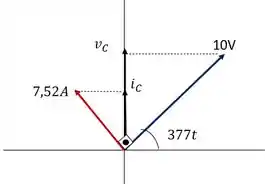
Pronto esse é o caso de corrente alternada pra um circuito de carga capacitiva.
Circuito de Carga Indutiva
Aqui, temos um circuito com um indutor e um gerador de corrente alternada.
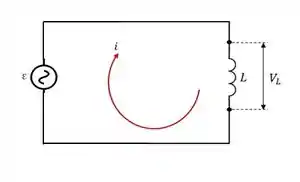
Onde .
Utilizando o mesmo princípio de regra das malhas, temos que a variação do potencial nos terminais do indutor se dá assim:
Para um indutor no qual a corrente varia à taxa , temos:
Substituindo a primeira equação na segunda e integrando em relação a , vemos que a corrente é dada por:
Aqui aparece uma nova grandeza, a reatância indutiva, definida por:
Além disso, vamos substituir por . A corrente deve ficar assim:
Onde é a amplitude da corrente, portanto:
E o diagrama fasorial desse cara ficaria da seguinte forma:
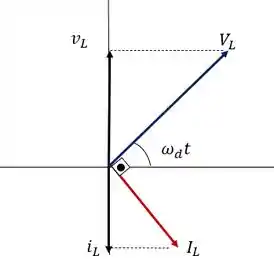
O processo de cálculo do circuito com indutor é muito parecido com o processo do circuito com capacitor, só o que muda é que a reatância é indutiva e a corrente ao invés de ser adiantada aqui é atrasada de em relação a voltagem.
Então vamos fazer uns exercícios pra ficar fera nessa matéria, já é?
Circuito de Carga Capacitiva
Circuito de Carga Indutiva
Exercícios Resolvidos
Exercício Resolvido #1
UFF – Lista 6 – Questão nº2.
Considere um resistor em série com uma fonte de . O gráfico da corrente e voltagem na resistência está dado na figura. Determine:
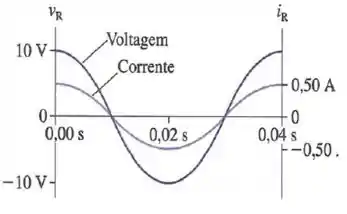
A frequência da .
O valor da resistência.
Passo 1
Pela análise do gráfico, podemos ver que o período é . Logo a frequência é dada por:
Passo 2
Par achar o valor da resistência, podemos usar a relação entre amplitude da corrente e amplitude da tensão, pois sabemos estes valores do gráfico, a relação nos diz:
Resposta
Exercício Resolvido #2
UFF – Lista 6 – Questão nº5.
Em um circuito formado por um indutor e uma fonte a reatância indutiva vale . A voltagem de pico da fonte vale . Sabendo que no instante a corrente instantânea vale , determine:
A frequência
A indutância do indutor.
Faça o gráfico dos fasores da corrente e das voltagens no indutor e na fonte.
Esboce o gráfico das funções e (os gráficos devem estar superpostos no mesmo sistema de eixos cartesianos).
Passo 1
Para determinar a frequência, podemos usar a equação da corrente em um circuito CA com carga indutiva:
Substituindo os valores dados no enunciado, temos:
Agora a gente tem que tirar o arcoseno dos dois lados da equação
Passo 2
Para determinar a Indutância, podemos usar a fórmula da definição da reatância indutiva:
Substituindo os valores, temos:
Passo 3
Para determinar o diagrama de fasores, precisamos lembrar que a corrente está atrasada em relação à tensão. Por ser apenas um circuito CA com um indutor, a tensão na fonte será a mesma tensão no indutor. Logo, o diagrama de fases para um tempo arbitrário será:
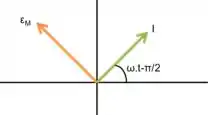
Passo 4
Para esboçar os gráficos de , e , vamos primeiro relembrar essas equações:
Logo, os gráficos ficaram:
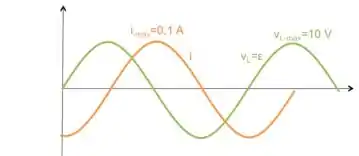
Resposta
Exercício Resolvido #3
Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 31, pp. 383
Suponha que se queira obter uma corrente de em um indutor puro de um circuito de rádio submetido a uma amplitude de voltagem de , com uma frequência de (correspondente ao limite superior da banda AM das frequências de rádio).
(a) Qual é a reatância indutiva necessária?
(b) Se a amplitude da voltagem for mantida constante, qual será a amplitude da corrente através de um indutor de ? E para ?
Passo 1
(a) Qual é a reatância indutiva necessária?
Bem, o circuito pode até ter outros elementos, mas neste exemplo não sabemos quais são. Tudo que eles fazem é fornecer ao indutor uma voltagem oscilante. Assim sendo, podemos simplesmente interpretá-los como uma fonte CA, beleza?
Vamos lá, sabemos que a reatância indutiva é dada por:
Passo 2
(b) Se a amplitude da voltagem for mantida constante, qual será a amplitude da corrente através de um indutor de ? E para ?
Para calcular a amplitude da corrente para diferentes frequências, vamos precisar do valor da indutância . Sabemos que:
Passo 3
A amplitude da corrente é dada por:
Para , temos que:
E para , temos que:
Resposta
(a)
(b) e .
Exercício Resolvido #4
Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 31, pp. 404
Um indutor de está conectado em série com um resistor de e uma fonte CA. A voltagem através do indutor é .
(a) Deduza uma expressão para a voltagem através do resistor.
(b) Qual é o valor de em ?
Passo 1
(a) Deduza uma expressão para a voltagem através do resistor.
Sabemos que a amplitude de voltagem no indutor é dada por:
Logo,
Já para o resistor, podemos escrever a seguinte expressão:
Substituindo os valores, temos que:
E isso significa que:
Passo 2
(b) Qual é o valor de em ?
Para , temos:
Resposta
(a)
(b) .