Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Momento Linear da Onda Eletromagnética

Ver Todos os Exercícios

Teoria

A luz carrega momento linear

Uma peculiaridade das ondas eletromagnéticas é que elas carregam momento linear.

Mas o que isso significa?

Imagina uma caneta de laser desligada. Quando a ligamos, ela emite luz pra frente. Como essa luz tem um momento linear γ → no sentido da propagação, pela conservação do momento, isso significa que a caneta tem que ir pra trás, com momento linear - γ → !

Então, a luz “carregar momento linear” significa que ela tem a capacidade de empurrar objetos!

Vamos ver qual é o momento linear da luz.

Quando a luz passa por uma região do espaço, ela “transfere” uma energia Δ U pra essa região.

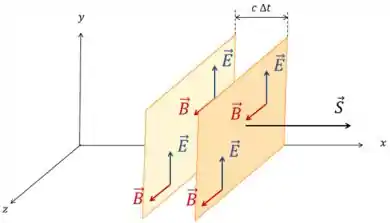
O momento linear da luz nessa região vai ser

γ → = Δ U c   k ^

Onde k ^ é o vetor unitário que dá a direção e o sentido de propagação da luz. Falando em escalares, a magnitude do momento linear da luz é:

γ = Δ U c

Agora, nem sempre um problema vai nos dar de bandeja a energia transferida. Nós precisamos calcular essa energia.

O fluxo médio de energia é dado pela intensidade I . Ela é a energia por unidade de tempo por unidade de área. Logo, a energia vai ser:

Δ U = I ∙ Δ t ∙ A

E o momento pode ser reescrito como:

γ = I ∙ A c   Δ t

Outra forma de reescrever o momento da luz é usando a potência da mesma. Potência ( P ) é energia por unidade de tempo. Logo, Intensidade é potência por unidade de área:

I = P A

P = I ∙ A

E vemos outra forma de reescrever o momento linear da luz.

γ = P c Δ t

O importante pra nós é que, no caso da caneta, a caneta iria pra trás com momento linear igual ao da luz! Como a velocidade da caneta dependeria da sua massa, temos:

p c a n e t a = m v = Δ U c

v = Δ U m c

Mas se a caneta iria pra trás, porque quando a gente liga o laser, não sentimos praticamente nada?

Porque o momento linear da luz é muito pequeno. A velocidade da luz é muito maior que a energia transferida.

Bem, agora enquanto você vai fazendo os exercícios de fixação, eu vou terminar de montar aqui minha nave movida a laser.

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 30-27

Uma pequena espaçonave cuja massa é 1,5 × 10 3   k g (incluindo um astronauta) está à deriva no espaço, longe de qualquer campo gravitacional.

Se o astronauta liga um laser de 10   k W de potência, que velocidade a nave atinge em 1,0   d i a por causa do momento associado à luz do laser?

Passo 1

O momento linear que a luz carrega é dado por:

γ = Δ U c

Onde Δ U é a energia que ela carrega em uma dada região do espaço. Mas nós não temos essa energia, nós temos apenas a potência do laser.

A potência da luz é a sua energia por unidade de tempo. Logo:

P = Δ U Δ t

Se substituirmos isso na nossa equação do momento, temos que em certo intervalo de tempo Δ t , a luz carrega um momento linear igual a:

γ = P c Δ t

Passo 2

Agora, vamos usar todos os dados que nós temos.

Primeiro vamos passar todas nossas informações para o Sistema internacional de Unidades (distâncias em metros, tempo em segundos, massa em quilogramas, etc....) para evitar complicações com unidade.

O laser fica ligado durante 1   d i a . Um dia tem 24   h o r a s , cada hora tem 60   m i n u t o s e cada minuto tem 60   s e g u n d o s .

1   d i a = 24 ∙ 60 ∙ 60 = 86   400   s e g u n d o s

Sabemos também a potência do laser P = 10   k W = 10 ∙ 10 3   W e a velocidade da luz c = 3 ∙ 10 8   m / s . Substituindo:

γ = 10 4 3 ∙ 10 8 ∙ 8,64 ∙ 10 4 ≅ 2,88   N ∙ s

Passo 3

Agora que já sabemos o momento linear que o laser adquire em um dia, usamos a lei da conservação do momento linear (pois não temos forças externas atuando no nosso sistema Nave-Laser).

Inicialmente, o momento linear era zero. Logo ele tem de ser sempre zero. Para isso, a nave tem que adquirir um momento igual ao da luz, mas com sentido oposto. Logo:

p n a v e = γ = 2,88   N ∙ s

Mas queremos saber a velocidade da nave! O enunciado afirma que a nave tem uma massa de 1,5 × 10 3   k g já com o astronauta. Vamos substituir na equação:

p n a v e = m ∙ v = 2,88   N ∙ s

v = 2,88 1,5 ∙ 10 3 = 1,92 ∙ 10 - 3   m / s

Resposta

A nave vai atingir uma velocidade de 1,92 ∙ 10 - 3 m / s = 1,92   m m / s após 1   d i a .

Exercício Resolvido #2

Elaboração própria

Uma estrela emite uma luz que atinge um meteoro e o movimenta. O meteoro possui massa de 10 10 K g e, após ser atingido, percorre um espaço de 1 metro em 1000 segundos. Determine:

  1. A variação de energia no percurso
  2. A potência da estrela

Passo 1

Começando pelo item a, podemos encontrar a variação da energia pensando na conservação do momento linear:

∆ U c = m v

∆ U   = m × v × c

A velocidade do meteóro pode ser calculada por:

v = ∆ x ∆ t = 1 1000

∆ U = 10 10 × 0,001 × 3 × 10 8 = 3 × 10 15 J

Passo 2

Pro item b, precisamos encontrar a potência da estrela. Para isso, basta dividirmos a variação da energia pelo tempo do percurso:

P o t = ∆ U ∆ t

P o t = 3 × 10 15 1000   = 3 × 10 12 W

Resposta

a ) 3 × 10 1 5 J

b) 3 × 10 12 W

Exercício Resolvido #3

Elaboração própria

Em um experimento, um laser foi apontado para uma placa, como mostra a figura abaixo:

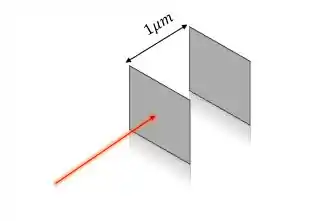
A placa se desloca 1 μ m . Se o laser possui potência de 200W e foi avaliado que o deslocamento durou 1 s , calcule:

  1. A massa da placa
  2. A densidade de momento linear da placa

Passo 1

Para o item a, vamos começar pelo mais simples, determinando a velocidade:

v = ∆ x ∆ t = 10 - 6 1 = 1 μ m / s

Para encontrarmos a massa, a gente ainda depende da variação da energia e podemos encontrá-la através da potência:

∆ U = P o t × ∆ t

∆ U = 200 × 1 = 200 J

Passo 2

Agora, podemos usar a conservação de momento linear e encontrar a massa da placa:

m v = ∆ U c

m = ∆ U v × c

m = 200 3 × 10 8 × 10 - 6 = 0,66 k g

Passo 3

Para o item b, a gente vai usar a fórmula da densidade do momento linear:

γ = ∆ U c

Como já conseguimos a variação da energia no item anterior e temos a velocidade da luz, agora é só substituir na equação e assim:

γ = 200 3 × 10 8 = 6,66 × 10 - 7 K g . m / s

Resposta

a ) 0,66 K g

b) 6,66 × 10 - 7 K g . m / s

Exercícios de Livros Relacionados

Em um teste para verificar se a magnetização de um sal paramagnético ao qual se aplica a curva da Fig. 32-14 obedece à lei de Curie, o sal é submetido a uma campo magnético de 0,50T , que permanece co
Um sal paramagnético ao qual a curva de magnetização da Fig. 32-14 se aplica é mantido à temperatura ambiente ( 300K ). Determine para que valor do campo magnético aplicado o grau de saturação magnéti
Uma barra magnética com 6,00c m de comprimento, 3,00m m de raio e uma magnetização uniforme de 2,70 ⋅ 10 3A / m pode girar em torno do centro como uma agulha de bússola. A barra é submetida a um campo
Considere um sólido com N átomos por unidade de volume, cada átomo com um momento dipolar magnético μ → . Suponha que existam apenas duas orientações possíveis para μ → : paralelo ou antiparalelo a um
Um pulso de laser tem energia de 20,0 Je o raio do feixe e de 2,00 mm.A duracao do pulso é 10,0 ns e a densidade de energiae uniformemente distribuida no interior do pulso.(a)Qualéa extensjo espacial