Análise Gráfica da Interferência por Meio de Propagação
Produzido por Bruno SoaresTeoria
Do que depende a interferência por meios de propagação?
Agora, vamos ver a interferência por meio de propagação através do amor número um de todos os cientistas no mundo: gráficos.
Como são os gráficos dessa interferência, e o que a gente pode extrair deles?
Para saber isso, precisamos relembrar as fórmulas que temos.
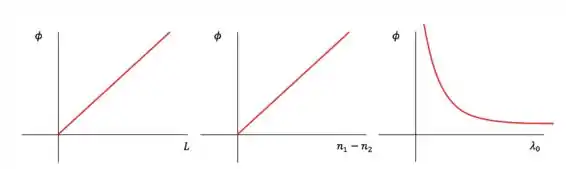
Primeiro, lembre que a diferença de fase é dada por:
O que podemos notar?
- A diferença de fase depende linearmente da espessura dos meios , cruzando o em (se a diferença de fase inicial for zero).
- A diferença de fase depende linearmente da diferença entre os índices de refração dos meios e .
- A diferença de fase é inversamente proporcional ao comprimento de onda da luz no vácuo, não cruzando nenhum eixo, mas tendendo para quando .
A intensidade resultante da interferência de dois raios de luz é dada pelo quadrado do cosseno de metade da diferença de fase entre eles (a interferência entre dois raios de luz é sempre dada por essa equação).
Logo, ela oscila com a espessura e o índice de refração dos meios e com o comprimento de onda da luz.
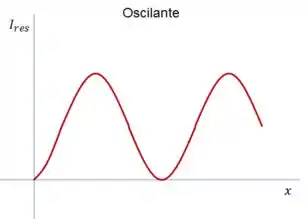
Onde os pontos de máximo são os de interferência totalmente construtiva ()
Os de mínimo são os de interferência totalmente destrutiva ().
Agora para os exercícios! (e por favor, sem álcool!)
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 106-84.
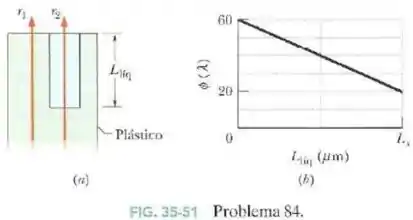
A Fig.35-51a mostra dois raios luminosos, com um comprimento de onda no ar de , que estão inicialmente em fase enquanto se propagam para cima em um bloco de plástico.
O raio atravessa o plástico e chega ao ar. Antes de chegar ao ar o raio passa por um líquido contido em uma cavidade do plástico. A altura do líquido é inicialmente , mas o líquido começa a evaporar.
Seja a diferença de fase entre os raios e ao chegarem ao ar. A Fig.35-51b mostra o valor de (em comprimentos de onda) em função da altura do líquido, com dado em termos de comprimentos de onda e a escala do eixo horizontal definida por . Determine:
- O índice de refração do plástico.
- O índice de refração do líquido.
Passo 1
Primeiro, vamos entender o problema.
Os dois raios luminosos se propagam, inicialmente, no mesmo meio (o plástico) e em fase até que o raio atinge a cavidade com líquido.
Assim, a diferença de fase entre eles na saída será devido a diferença de meio de propagação.
Contudo, é importante notar que, inicialmente, essa diferença de meio se dá apenas pelo líquido, mas a medida que o líquido evapora ela vai se dando pelo líquido e pelo ar na cavidade.
Passo 2
a)
A diferença de fase dada pela diferença de meio de propagação em múltiplos do comprimento de onda é dada por:
Pelo gráfico, temos diversos valores de para diversos valores de , e a altura de ar vai ser a altura da cavidade menos a altura do líquido. O problema também nos dá o comprimento de onda da luz incidente.
Para inverter a equação, e achar um dos dois índices de refração, é necessário ter o outro índice.
Tem um meio cujo índice de refração sabemos, mesmo sem o problema nos contar: o ar, cujo índice de refração é 1.
Passo 3
A medida que o líquido evapora, a cavidade vai ficando com ar dentro dela. Quando o líquido evaporar completamente () teremos apenas ar na cavidade que tem uma altura de (altura inicial do líquido). Temos então:
- (obtido na letra (a) )
Passo 4
b)
Para encontrar o índice de refração do líquido, podemos “inverter o tempo”. No início do processo, a cavidade tinha apenas o líquido (antes de ele evaporar). Com isso, podemos usar uma equação semelhante a anterior para achar o índice de refração do líquido usando o índice do plástico.
Passo 4
Os valores da equação nós já temos. Lembrando que a diferença de fase nós tiramos do gráfico (neste caso, usamos , o extremo direito do gráfico )
Resposta
a)
b)
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 107-90.
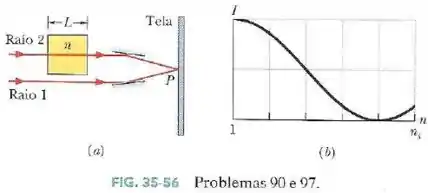
Na Fig.35-56a, as ondas associadas aos raios e estão inicialmente em fase e têm o mesmo comprimento de onda no ar. O raio atravessa um material de comprimento e índice de refração .
Os raios são em seguida refletidos por espelhos para um ponto comum , situado sobre uma tela. Suponha que é possível fazer variar de até . Suponha também que de a a intensidade da luz no ponto varia com da forma indicada na Fig.35-56b.
Para que valores de maiores que a intensidade :
- É máxima?
- É zero?
- Que múltiplo de corresponde à diferença de fase entre os raios no ponto para ?
Passo 1
a)
Quando a interferência é totalmente construtiva a intensidade é máxima, e quando é totalmente destrutiva a intensidade é mínima.
As condições para isso quando temos uma diferença de fase por meio de propagação são:
Interferência construtiva:
Interferência destrutiva:
Lembrando que o raio está sempre no ar, temos que (o índice de refração do ar é aproximadamente 1).
Passo 2
Para sabermos quando que a interferência será construtiva ao variarmos precisamos encontrar a razão .
Pelo gráfico de intensidade, sabemos que é o primeiro índice de refração acima de 1 que causa interferência destrutiva. Logo, para este valor, .
Passo 3
Agora, para acharmos os valores de com interferência construtiva (intensidade máxima), vamos variando até passarmos de (evitamos pois ele corresponde a ). Rearranjando a condição:
Onde e .
E paramos por aqui, pois .
Passo 4
b)
A intensidade zera para o caso de interferência totalmente destrutiva. Manipulando um pouco a condição de interferência destrutiva:
Como tínhamos calculado no item anterior, e . Novamente, vamos testando diversos valores de depois do 0 até ultrapassarmos o limite de índices de refração possíveis.
Para , e por isso paramos por aqui.
Passo 5
c)
A diferença de fase em múltiplos do comprimento de onda é dada por:
Dos itens anteriores, sabemos que e por isso .
Resposta
a)
A intensidade é máxima para .
b)
A intensidade é zero para .
c)
A diferença de fase dos raios no ponto para é de comprimentos de onda.
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 108-97.
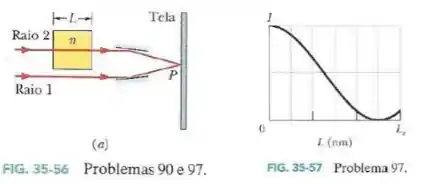
Na Fig.35-56a, as ondas associadas aos raios e estão inicialmente em fase e têm o mesmo comprimento de onda no ar. O raio atravessa um material de comprimento e índice de refração . Os raios são refletidos por espelhos para um ponto comum , situado sobre uma tela.
Suponha que seja possível fazer variar de até . Suponha também que de até a intensidade da luz no ponto varia com da forma indicada na Fig.35-57.
Para que valores de maiores que a intensidade :
- É máxima?
- É zero?
- Que múltiplo de corresponde à diferença de fase entre os raios no ponto para ?
Passo 1
Existem mais de uma forma de resolver um mesmo exercício.
Primeiro, podemos resolver esse exercício de forma metódica: usamos as condições de interferência construtiva e destrutiva junto com o gráfico de intensidade em função de para encontrar os valores necessários para o problema.
Mas existe uma outra forma de resolver também, que é usando as oscilações do gráfico de intensidade. Vamos seguir por esse caminho.
Passo 2
a)
A intensidade da onda resultante da interferência de duas ondas eletromagnéticas depende do cosseno da diferença de fase entre as duas.
Onde a diferença de fases é dada por
Note que depende diretamente da espessura do meio 2.
Sabemos então que o gráfico da intensidade contra vai se repetindo sempre!
Passo 3
Se o gráfico se repete, então a distância entre o primeiro máximo e o primeiro mínimo de intensidade e a distância entre o primeiro mínimo e o segundo máximo de intensidade serão iguais.
Como o “primeiro máximo” é dado pra , essa distância é de (pelo gráfico).
Logo, o segundo máximo está em .
Se a gente repetir essa ideia pra máximos adjacentes subsequentes, veríamos que os máximos do segundo em diante correspondem a:
Onde corresponde ao nosso segundo máximo.
Passo 4
b)
Repetiremos a mesma ideia do item anterior. O primeiro mínimo corresponde a . A distância até o segundo mínimo é a distância até o segundo máximo (), e desse até o segundo mínimo ().
O segundo mínimo então está em .
Para outros máximos, nós somamos mais e depois mais e mais e mais...
Onde corresponde ao nosso segundo mínimo.
Passo 5
c)
Na letra (a), encontramos que o primeiro máximo após é dado por .
Como o máximo é quando temos uma diferença de fase como um múltiplo inteiro do comprimento de onda, e como esse é o primeiro, podemos dizer que neste caso a diferença de fase corresponde a 1 comprimento de onda.
A quantos comprimentos de onda a diferença de fase para corresponde pode ser achado por uma regra de 3 (podemos usar isso pois ela é linear com ).
Resposta
a)
A intensidade é máxima para .
b)
A intensidade é zero para .
c)
A diferença de fase dos raios no ponto para é de comprimentos de onda.