Interferência por Meio de Propagação
Produzido por Bruno SoaresTeoria
Diferentes meios de propagação
Vamos montar em casa dois pontos de Wi-Fi, um na sala e outro no corredor, pra pegar melhor no meu quarto.
Meu quarto fica no meio dos dois, e eu estava usando a internet sem problemas, até que minha mãe colocou um balde transparente de água entre os dois, e do nada, minha internet não funciona mais! Que droga foi essa?
A luz se propaga com diferentes velocidades em diferentes meios
Quando ondas eletromagnéticas saem de duas fontes em fase, não é só a diferença de caminho que pode atrapalhar as duas: os meios pelos quais elas se propagam também podem tirá-las de fase...
Acontece que, quando a luz passa pela água sua velocidade diminui, o que faz com que o caminho dela não seja mais equivalente a quando ela está se propagando só no ar. Isso é por causa da refração!

A velocidade da luz no ar, na água, em um cristal, em óleo, ou em outros meios é diferente para cada um, e é medida pelo índice de refração de cada um. Quanto maior o índice de refração, menor a velocidade da luz no meio.
Diferença de fase para dois meios diferentes
Para acharmos as condições de interferência nesse caso, vamos jogar dois feixes de laser num copo com água e óleo, e checar se na saída eles estão ou não em fase.
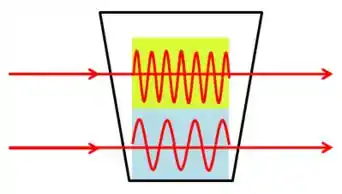
Uma coisa importante de se considerar, que está representado na imagem, é que o comprimento de onda da luz no óleo e na água é diferente. Assim como a velocidade, quanto maior o índice de refração, menor o comprimento de onda.
Onde é o comprimento de onda da luz no vácuo.
Agora, vamos ver qual a diferença de fase em múltiplos do comprimento de onda. Considere que o óleo e que a água tem mesma espessura . Vamos chamar o óleo de e a água de . Assim, o número de comprimentos de onda no óleo e na água são:
Ok... e a diferença de fase?
Bem, agora a gente subtrai! (Considerando que )
Sendo que se a diferença de fase for de um número inteiro de comprimentos de onda, a interferência é construtiva. Se for um múltiplo de meio comprimento de onda, a interferência é destrutiva. (no caso dos sinais terem mesma amplitude)
Também podemos passar isso para radianos! Como a diferença de fase para um comprimento de onda é , para o nosso caso vai ser:
E para aqueles casos mais importantes, de interferência destrutiva e construtiva?
Para a destrutiva:
Para a construtiva:
Mas afinal, e para o caso da minha mãe com o balde de água?
O caminho no balde não é igual ao caminho no ar!
Bem, neste caso em específico, fora a parte do balde, o resto dos caminhos no ar são iguais. Ou seja, só vai importar mesmo a diferença de fase por meio de propagação.
Mas se esses caminhos restantes fossem diferentes, então você teria que ver a diferença de fase por causa do meio de propagação e por causa da diferença de caminhos!
Tendo as duas, você pode somá-las!
Agora vamos para os exercícios, pra ficar monstrão! No pain no gain!!!
Diferença de fase para dois meios diferentes
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 100-5.
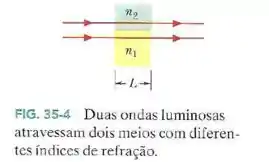
Na Fig. 35-4, suponha que duas ondas com um comprimento de onda de , que se propagam no ar, estão inicialmente em fase.
Uma atravessa uma placa de vidro com um índice de refração e espessura ; a outra atravessa uma placa de plástico com um índice de refração e a mesma espessura.
- Qual é o menor valor de para a qual as ondas deixam as placas com uma diferença de fase de ?
- Se as ondas chegam ao mesmo ponto com a mesma amplitude, a interferência é totalmente construtiva, totalmente destrutiva, mais próxima de construtiva ou mais próxima de destrutiva?
Passo 1
a)
Inicialmente, veja que os dois raios de luz atravessam a mesma distância nos meios com diferentes índices de refração.
Logo, a diferença de fase entre os dois será dada apenas por essa diferença de índice de refração. Como vimos, ela será dada (em radianos) por:
Passo 2
Agora, para usar essa equação, o problema nos dá algumas informações:
Índice de refração do meio 1:
Índice de refração do meio 2:
Comprimento de onda da luz no vácuo:
Diferença de fase na saída:
Assim, substituindo na equação, temos:
Passo 3
Uma observação: por que o problema diz que esse é o “menor valor de ” para essa diferença de fase?
Porque outros valores possíveis seriam , , e por aí vai. Peraí, como assim?!
Acontece que, se somarmos na nossa diferença de fase, nós temos “fisicamente” a mesma situação! Os pontos de uma onda correspondentes ao da outra continuariam sendo os mesmos. Em questões de comprimento, isso equivale a termos mais .
Passo 4
b)
Uma diferença de fase de meio comprimento de onda, que causa interferência totalmente destrutiva, é equivalente a uma diferença de fase de .
Uma diferença de fase de um comprimento de onda, que causa interferência totalmente construtiva, é equivalente a uma diferença de fase de .
Avaliando a nossa diferença de , ela é mais próxima de ser totalmente construtiva.
Resposta
a)
b)
A interferência é mais próxima de totalmente construtiva.
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 101-11
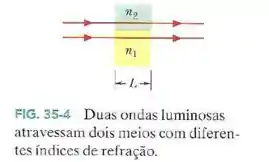
Na Fig. 35-4, suponha que as duas ondas luminosas, cujo comprimento de onda no ar é , têm inicialmente uma diferença de fase de . Os índices de refração dos materiais são e . Determine:
- O menor valor de para o qual as duas ondas estão exatamente em fase depois de atravessar os dois materiais.
- O segundo menor valor de para o qual as duas ondas estão exatamente em fase depois de atravessar os dois materiais.
Passo 1
a)
As ondas inicialmente têm uma diferença de fase .
Além disso, após atravessarem os dois materiais teremos mais uma diferença, devido à diferença de índice de refração dos materiais:
Logo, a diferença de fase total será:
Para eles estarem exatamente em fase, eles devem ter uma diferença de fase de um múltiplo inteiro de . Isso significa que a diferença de fase vai ser de:
Passo 2
O problema nos dá os índices de refração dos materiais, e , e o comprimento de onda da luz incidente no vácuo, .
O menor valor de é aquele dado pela menor diferença de fase possível, que corresponde a . Assim:
Passo 3
b)
Se eu pegar uma diferença de fase e somar , a situação física é a mesma. Como a diferença de fase para interferência construtiva é de , sempre que eu somar a ela eu terei de novo a mesma situação! Por isso que colocamos como condição que .
Com isso, o segundo menor valor de possível corresponde a . Assim:
Resposta
a)
b)
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 101-13.
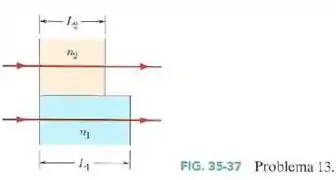
Duas ondas luminosas no ar, de comprimento de onda , estão inicialmente em fase. As ondas passam por camadas de plástico, como na Fig.35-37, com , , e .
- Qual é a diferença de fase, em comprimentos de onda, quando as ondas saem dos dois blocos?
- Se as ondas são superpostas em uma tela, com a mesma amplitude, a interferência é totalmente construtiva, totalmente destrutiva, mais próxima de construtiva ou mais próxima de destrutiva?
Passo 1
a)
Neste caso, a situação do problema mudou um pouco, pois o comprimento de cada meio é diferente. Mas tem uma forma de passarmos por cima disso.
Vamos considerar um meio 3 (o ar) logo depois do meio 2, e considerar a diferença de fase causada pela passagem por 2 em comparação a 1 e depois do meio 3 em comparação ao 1.
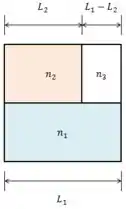
As equações serão, em múltiplos do comprimento de onda:
A diferença de fase total será a soma das duas.
Passo 2
De acordo com o enunciado, temos que , e, como o meio 3 é ar, podemos aproximar seu índice de refração por .
O comprimento de onda da luz incidente é de e a largura de cada meio é e .
A diferença de fase é de 0,833 comprimentos de onda.
Passo 3
b)
A interferência é totalmente destrutiva quando ela é um múltiplo inteiro do comprimento de onda acrescido de meio comprimento de onda (), enquanto ela é totalmente construtiva quando ela é um múltiplo inteiro do comprimento de onda.
Como a diferença de fase está mais próximo de 1 comprimento de onda que de 0,5 comprimentos de onda, a interferência é mais próxima de construtiva.
Resposta
a)
A diferença de fase é de comprimentos de onda.
b)
A interferência está mais próxima de ser construtiva.