Espelhos Planos
Produzido por Ludovic BeghinTeoria
Espelho é uma superfície que reflete o raio luminoso em uma direção definida, em vez de absorvê-lo ou espalhá-lo em todas as direções.
Vamos entender nesse capítulo as imagens formadas por espelhos planos.
Vamos imaginar uma fonte de luz pontual a uma distância de um espelho plano. Um raio luminoso que sai do ponto e incide com um ângulo com a normal ao espelho, refletirá com o mesmo ângulo com a normal.
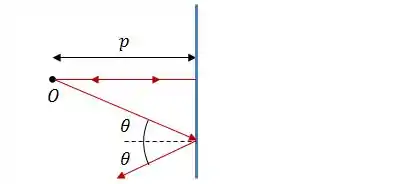
Quando fazemos o prolongamento no sentido inverso dos raios refletidos, podemos ver que eles se interceptam em um mesmo ponto que está a uma distância do espelho. Esse ponto é a imagem do objeto , se liga:
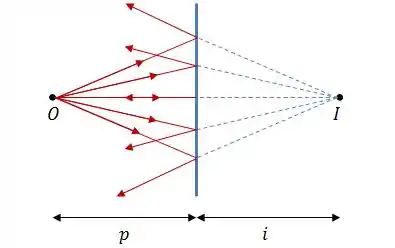
No caso do espelho plano, as imagens formadas são chamadas de imagens virtuais, pois nenhum raio passa realmente pelo local onde a imagem se encontra, ou seja, a imagem se forma atrás do espelho.
Por convenção, as distâncias dos objetos serão sempre positivas e as distâncias das imagens serão sempre negativas. Assim, para um espelho plano, a distância do objeto ao espelho será sempre igual ao módulo da distância da imagem ao espelho . Então, podemos dizer que:
Espelho Plano + Mudança de Meio
Imagina o problema descrito pela figura abaixo. A que distância do espelho será formada a imagem?

Temos que levar em consideração tanto os efeitos de um espelho plano quanto os de refração!
O primeiro passo aqui é saber escolher dois raios luminosos para achar a interseção de seus prolongamentos.
Quando o feixe luminoso passa do ar para a água perpendicularmente a luz não sofrerá desvio. Então vamos escolher esse raio primeiro.
Um outro bom feixe para trabalharmos é tal que os ângulos sejam bem pequenos. Dessa forma:
Desenhando o ponto de encontro dos feixes luminosos (que é onde a imagem será formada), vamos ter o gráfico abaixo, que nos permite enxergar a geometria do problema.
Para ajudar na nossa análise, definimos os pontos , e onde o feixe de luz passa pela interface ar/água e o ponto em que o feixe reflete no espelho.
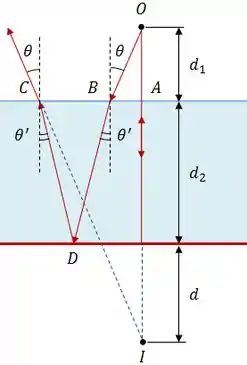
Sabendo que os ângulos ( e ) são suficientemente pequenos e que o índice de refração do ar é igual a 1, de acordo com a Lei de Snell, teremos:
Agora vamos basicamente fazer a análise de triângulos para calcular a distância .
- Triângulo :
- Triângulo :
- Triângulo :
Vemos que:
O que nos dá:
Substituindo :
Daqui podemos tirar que
Opa! Podemos substituir as relações para os lados e na primeira equação.
Finalmente:
Dessa relação, podemos ver que a distância entre a imagem e o espelho independe do ângulo que escolhermos para desenhar os nossos feixes, assim como deve ser.
Rotação de Espelho Plano
Vamos começar olhando uma simples reflexão de um raio luminoso, que sai da fonte pontual , em um espelho plano:
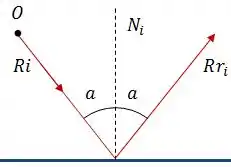
Onde é o raio incidente, é o raio refletido na posição inicial e é a linha normal ao espelho na posição inicial.
Até aqui nenhuma novidade, certo?
A situação em que estamos interessados aqui é a de quando ocorre uma rotação do espelho de um ângulo , como na figura abaixo:
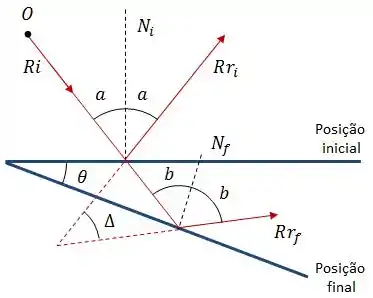
Nesse caso, qual é o ângulo formado pelos prolongamentos dos raios refletidos?
Um detalhe importante e que pode ser que não seja muito nítido é a relação entre os ângulos , e , que é dada por:
A partir disso, vamos analisar o triângulo formado pelos prolongamentos dos raios refletidos:
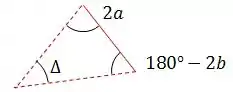
A soma dos ângulos internos de um triângulo deve ser sempre igual a , logo:
Agora é só dar uma arrumada nisso:
Finalmente:
Assim, os raios refletidos sempre girarão o dobro do ângulo de rotação do espelho.
Combinação de Espelhos Planos
Vamos começar imaginando dois espelhos planos que formam entre si um angulo , entre os espelhos colocamos um objeto .
Os feixes de luz que vem desse ponto sofrem reflexão regular nos dois espelhos, formando duas imagens virtuais. No entanto, os raios que se refletem em um espelho incidem sobre o outro, e cada ponto imagem acaba funcionando como um novo ponto objeto e, com isso, formando novas imagens virtuais.
Para cada ângulo existe um número determinado de imagens , dado por:
Fisicamente, acontece o seguinte:
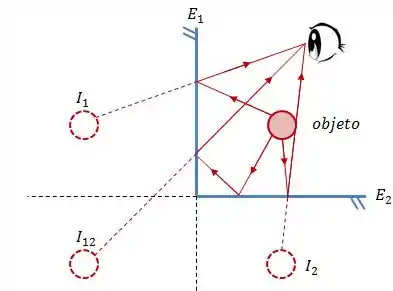
Visualmente, o resultado é esse:

Esse é o caso simples, em que temos apenas dois espelhos planos combinados. Podemos ter um caso mais complexo que é quando temos um verdadeiro labirinto de espelhos. Agora, vamos dar uma olhada nos exercícios que você vai pegar o jeito da coisa! =)
Espelho Plano + Mudança de Meio
Rotação de Espelho Plano
Combinação de Espelhos Planos
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
Uma mariposa está no nível dos seus olhos, a de distância de um espelho plano; você se encontra atrás da mariposa, a do espelho.
Qual é a distância entre os seus olhos e a posição aparente da imagem da mariposa no espelho?
Passo 1
A mariposa está a do espelho, logo, será formada uma imagem atrás do espelho plano.
Como você está a do espelho, a distância entre você e a imagem da mariposa será:
Resposta
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
A figura abaixo mostra uma vista de topo de um corredor com um espelho plano montado em uma das extremidades.
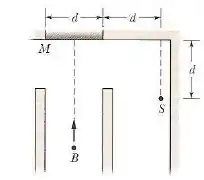
Um ladrão se esgueira por um corredor em direção ao centro do espelho. Se , a que distância o ladrão está do espelho no momento em que é avistado pelo vigia ?
Passo 1
Quando o vigia for capaz de ver o ladrão , o raio luminoso proveniente de deve refletir na beira do espelho:
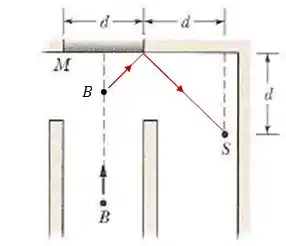
Devido à geometria do problema, o ângulo de reflexão deve ser de :
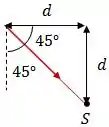
A partir disso, podemos descobrir a distância que o ladrão estará do espelho.
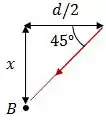
Onde . Logo:
Resposta
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
A figura abaixo mostra uma pequena lâmpada pendurada a uma distância acima da superfície da água de uma piscina na qual a profundidade da água é . O fundo da piscina é um espelho.
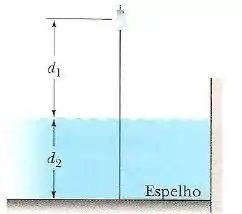
A que distância da superfície do espelho está a imagem da lâmpada?
(Sugestão: Construa um diagrama de dois raios, mas leve em conta o desvio dos raios luminosos causado pela refração. Suponha que os raios não se desviem muito de uma reta vertical passando pela lâmpada e use a aproximação, válida para pequenos ângulos, de que .)
Passo 1
Fazendo exatamente as mesmas considerações que fizemos na teoria, chegaremos à seguinte fórmula:
Onde:
Logo:
Resposta
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 74
Prove que se um espelho plano for girado de um ângulo o raio refletido girará de um ângulo . Mostre que esse resultado é razoável para .
Passo 1
A situação é basicamente essa:
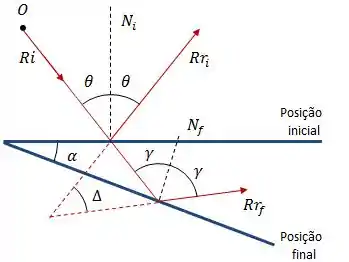
Onde é o ângulo de rotação do raio refletido.
Passo 2
Um detalhe importante e que pode ser que não seja muito nítido é a relação entre os ângulos , e , que é dada por:
A partir disso, vamos analisar o triângulo formado pelos prolongamentos dos raios refletidos:
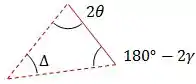
A soma dos ângulos internos de um triângulo deve ser sempre igual a , logo:
Reorganizando isso, teremos:
Onde :
Passo 3
Assim, se o ângulo de rotação for de , o raio refletido girará em .
Para mostrar que é razoável, vamos começar imaginando a situação em que o raio incide sobre uma superfície com um ângulo de incidência inicial de .
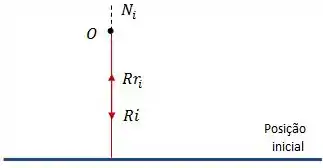
Agora vamos ver o que acontece quando giramos o espelho em .
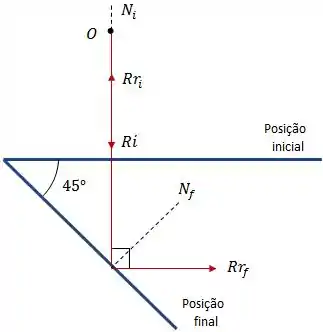
Como podemos ver na imagem acima, o raio refletido final teve uma rotação de em relação ao raio refletido inicial.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 71
Dois espelhos planos paralelos estão separados por uma distância de . Um objeto é colocado a de um dos espelhos.
Determine a menor; a segunda menor; a terceira menor (ocorre duas vezes) e a quarta menor distância entre o objeto e sua imagem.
Passo 1
Determine a menor distância entre o objeto e sua imagem.
Vamos chamar de o espelho mais próximo do objeto, e de o espelho mais afastado do objeto.
No espelho , a imagem está atrás de e, portanto, a do objeto. Essa é a menor distância.
Passo 2
Determine a segunda menor distância entre o objeto e sua imagem.
O espelho reflete tanto a o objeto quando a imagem .
O objeto está a de e formará uma imagem que está atrás do espelho. Assim, a distância entre a imagem e o objeto é de .
Essa é a segunda menor distância.
Passo 3
Determine a terceira menor (ocorre duas vezes) distância entre o objeto e sua imagem.
A terceira menor distância será o resultado da reflexão de no espelho .
A imagem está atrás de , e a distância entre e é de . Logo, está a de .
Assim, será formada uma imagem que está atrás do espelho .
Como a distância entre e o objeto é de , a distância entre o objeto e será de .
Obs.: Se usarmos o mesmo raciocínio, mas dessa vez na reflexão da imagem no espelho , veremos que será formada uma imagem com a mesma distância para o objeto. É por isso que o enunciado diz que este caso ocorre duas vezes.
Passo 4
Determine a quarta menor distância entre o objeto e sua imagem.
O próximo caso é a reflexão da imagem no espelho .
está atrás de , e está a de . Assim, será formada uma imagem que está atrás de .
Como a distância entre o objeto e é de . A imagem estará a do objeto.
Resposta
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 65
Na figura abaixo uma fonte luminosa pontual e isotrópica é posicionada a uma distância de uma tela de observação e a intensidade luminosa no ponto (na mesma altura que ) é medida.
Em seguida, um espelho plano é colocado atrás de , a uma distância .

De quantas vezes aumenta a intensidade luminosa quando o espelho é introduzido?
Passo 1
Esse exercício exige que você saiba a relação entre a intensidade luminosa e a distância entre a fonte e o receptor. Qual é essa relação?
A intensidade luminosa é inversamente proporcional ao quadrado da distância entre a fonte e o receptor! Logo, podemos escrever a intensidade da fonte como:
Onde é uma constante de proporcionalidade.
Passo 2
Vamos olhar agora para a luz refletida. Entre sair do ponto , refletir no espelho e chegar ao anteparo , a luz percorre uma distância igual a .
Logo, a intensidade luminosa da luz refletida será dada por:
Passo 3
A intensidade resultante será a soma das intensidades, logo:
Assim, a intensidade aumentará em vezes
Resposta
A intensidade aumentará em vezes
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 72
A figura abaixo é uma vista de topo de dois espelhos planos verticais com um objeto entre eles.
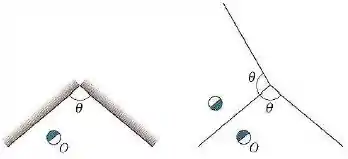
Quando um observador olha para os espelhos vê múltiplas imagens do objeto. Para determinar as posições dessas imagens desenhe o reflexo em cada espelho da região entre os espelhos, como foi feito para o espelho da esquerda na figura da direita.
Em seguida, desenhe o reflexo do reflexo. Continue da mesma forma do lado esquerdo e do lado direito até que os reflexos se cruzem ou se superponham do lado de trás dos espelhos. Quando isso acontecer, basta contar o número de imagens de .
Determine o número de imagens formadas para ; ; .
Para , determine o menor e o maior número de imagens que podem ser observadas, dependendo do ponto de vista do observador da posição do objeto .
Para cada situação, indique as posições e orientações de todas as imagens de em um desenho semelhante ao da figura acima.
Passo 1
Determine o número de imagens formadas para .
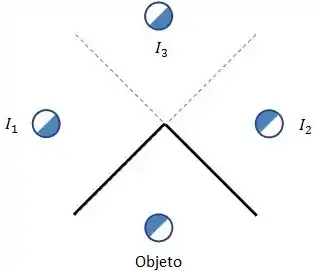
Outra forma de resolver o problema é aplicando a seguinte equação:
Para :
Passo 2
Determine o número de imagens formadas .
Para :
Passo 3
Determine o número de imagens formadas .
Para :
Passo 4
Para , determine o menor número de imagens que podem ser observadas, dependendo do ponto de vista do observador da posição do objeto .
Para o número total de imagens formadas é dada por:
Assim, se o observador olhar o sistema de modo que ele, o objeto e uma das imagens estejam na mesma linha, ele só poderá ver .
Passo 5
Para , determine o maior número de imagens que podem ser observadas, dependendo do ponto de vista do observador da posição do objeto .
O número máximo de imagens que podem ser observadas é justamente e o número de imagens formadas. Nesse caso, .
Resposta