Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Partícula na Caixa Unidimensional

Ver Todos os Exercícios

Teoria

Fala aí!!! Seja muito bem vindo ao Responde Aí! Bora entender juntos tudo sobre Partícula na Caixa Unidimensional?!

Um dos problemas mais tradicionais da mecânica quântica é o de uma partícula, como o elétron, confinada numa “caixa” unidimensional de comprimento.

Esse problema é descrito pela Equação de Schrödinger independente do tempo para uma caixa unidimensional e hoje vamos entender o que é isso e como resolver esse problema!

Pra começar, vamos dar uma olhadinha na Equação de Schrödinger independente do tempo!

Equação de Schrödinger independente do tempo

Indo direto ao ponto, a Equação de Schrödinger independente do tempo é dada por:

Onde:

  • é a constante reduzida de planck que tem a seguinte relação:
  • é a função de onda independente do tempo;
  • é o potencial de cada região;
  • é a massa da partícula.
  • é a energia da partícula.

Beleza, agora podemos entender quem é essa tal de Caixa Unidimensional!

Partícula num poço de potencial infinito

O que a gente chama de “caixa” é uma armadilha para pegar ratos, digo, elétrons. 🤣

Nós fazemos um poço de potencial infinito, que se descreve matematicamente da seguinte forma:

$$U(x)=\left\{\begin{matrix}\infty&x<0\0&00\end{matrix}\right.$$

Graficamente, o que acontece é o seguinte:

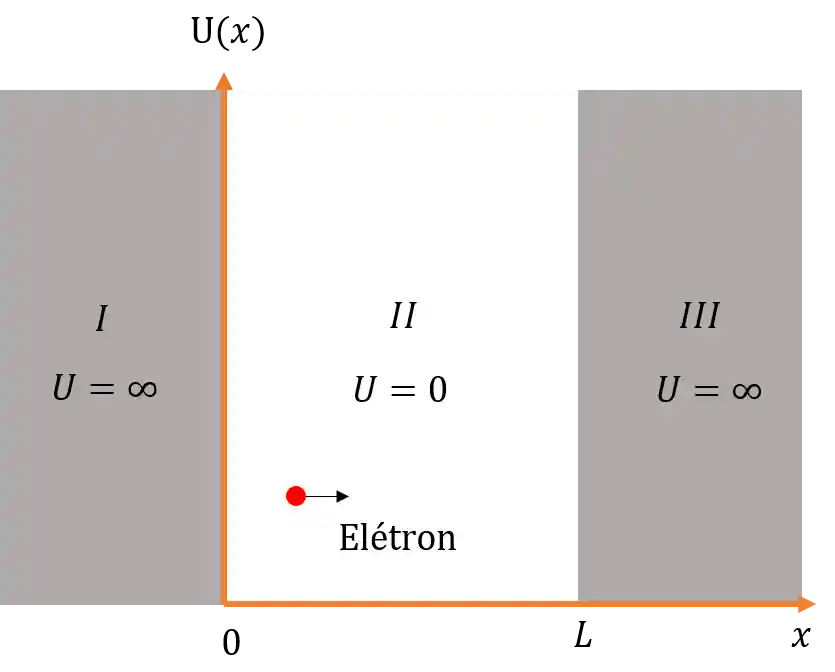
Elétron em uma caixa unidimensional
Elétron em uma caixa unidimensional

Ou seja a energia na regiões l e lll fora da caixa tem potencial infinito e a região I, dentro da caixa tem o potencial igual a zero. Vamos entender a diferença de potencial.

Equação de Schrödinger para as Regiões I e III

Fazendo constante, podemos observar que uma solução dessa equação é:

Onde .

Se fizermos , então .
Logo, fora da caixa, a função de onda tem que ser zero.

Equação de Schrödinger para a Região II

Temos a seguinte condição de contorno, considerando que a função de onda é zero fora da caixa e que ela é continua em todo o espaço nos dá as seguintes condições de contorno:

No interior da caixa e teremos:

Onde é uma rearrumação das constantes conhecidas dada por:

Resolvendo essa equação diferencial e utilizando as condições de contorno encontramos:

Onde . O valor de  é determinado a partir da condição de normalização:

O que nos da:

Assim a função de onda, dada por:

Onde  é o número quântico da partícula na caixa e é inteiro, mostrando que os estados possíveis da partícula são quantizados.

Função densidade de probabilidade

Essa função determina a probabilidade do elétron estar numa determinada posição na caixa, e é encontrada elevando a função de onda ao quadrado porém em módulo.

Os gráficos dessa função possuem um jeito muito fácil de se esboçar. Mais importe do que calcular a função é entender que o número de cristas é proporcional ao número .

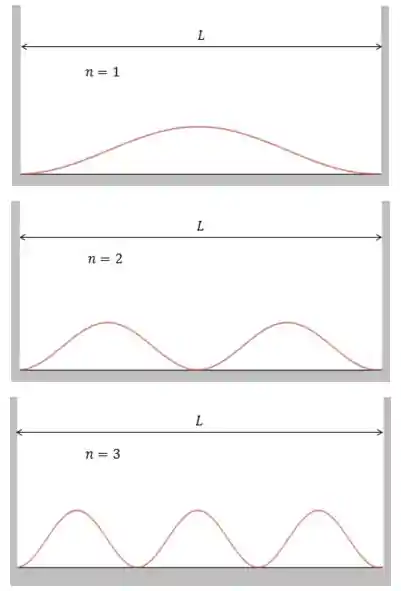
Função densidade de probabilidade.
Função densidade de probabilidade.

As extremidades da caixa são sempre um nó (pontos onde ) por causa das condições de contorno. Além disso, dentro da caixa, terão sempre nós, totalizando nós. A gente pode usar como exemplo essas figuras dos estados, vamos pegar pra .

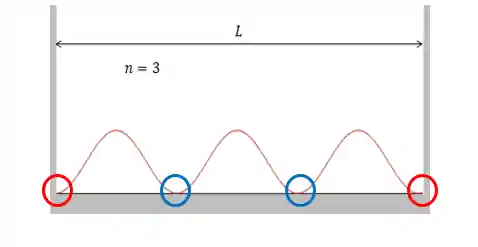
Nós da função de probabilidade.
Nós da função de probabilidade.

Na caixa:

ó
ó

Total de nós:

ó
ó

Esses nós correspondem a:

E isso rola pois quando o a função também será já que é uma constante multiplicando um seno.
Pra o argumento dentro dele deverá ser

E rearrumando em função da posição a gente encontra uma equação pra posição dos nós:

Para que esteja na região , é sempre menor ou igual a .
Teremos também picos, que correspondem a:

Obs: O  entra também na jogada por que os picos aparecem quando a densidade é máxima, e a densidade é dada a partir do . Sabendo que a função seno varia de  até ,  o  terá seu máximo á  quando o  e quando o .

Pra esse seno ser o argumento dentro do seno tem que ser

Enfim conseguimos uma equação para a posição dos picos:

Dessa vez precisamos que para ficar na região .

Vamos usar como exemplo e vamos calcular a posição dos nós e dos picos a gente viu pela figura que são nós.
Para os nós substituímos os valores de de até , na equação:

Para :

Para :

Para :

Para :

A gente viu que são picos, então usaremos a equação dos picos e vamos substituir os valore de m no intervalo de até .

Como :

Substituímos :

Energia da Partícula na Caixa

Ao resolvermos a equação de Schrödinger, tivemos que fazer:

Porém, quando montamos a equação, tínhamos:

Como os valores de da solução final são quantizados, então os níveis de energia da partícula também vão ser quantizados!

Substituindo , temos

Atenção aqui, essa fórmula é bastante usada e será bem importante pra encontrar a energia do elétron em diferentes estados.

Para nós temos a energia do estado fundamental:

Enquanto que para qualquer outro estado de energia:

Exemplo:

A gente pode agora fazer um exemplo aqui rápido, imagina que a energia no estado fundamental é qual será a energia no terceiro estado excitado?
Para o terceiro estado a gente tem:

Aplicando na fórmula o valor de .

Prontinho!

Agora eu vou te deixar com um resumindo em vídeo!

Vamos praticar com exercícios?!

Função densidade de probabilidade

Energia da Partícula na Caixa

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 240-13.

Um elétron que está confinado em um poço de potencial infinito unidimensional de largura L é excitado do estado fundamental para o primeiro estado excitado.

Essa excitação aumenta, diminui ou não tem nenhum efeito sobre a probabilidade de detectar o elétron em uma pequena região:

  1. No centro do poço?
  2. Perto de uma das bordas do poço?

Passo 1

Vamos resolver esse problema com argumentos mais qualitativos, lembrando que a função de onda para o elétron confinado é:

ψ n ⁡ x = 2 / L ∙ sen ⁡ n π L ∙ x

E a densidade de probabilidade de encontrar o elétron é:

ψ n 2 ⁡ x = 2 L ∙ sen 2 ⁡ n π L ∙ x

A probabilidade de encontrar o elétron em uma região vai ser:

∫ a b ψ n 2 x d x

Obs: Você poderia tentar deduzir a fórmula exata da probabilidade e tentar comparar para os dois estados, mas essa análise seria bem mais complicada.

Passo 2

Letra a)

No estado fundamental, temos n = 1 e a densidade de probabilidade fica:

ψ 2 ⁡ x = 2 L ∙ sen 2 ⁡ π L ∙ x

O gráfico fica:

O primeiro estado excitado corresponde a n = 2 .

ψ 2 ⁡ x = 2 L ∙ sen 2 ⁡ 2 π L ∙ x

No primeiro gráfico é possível ver que ψ 2 está mais concentrado no centro da figura, enquanto na segunda o centro tem um mínimo.

Isso significa que a probabilidade de detectar o elétron numa pequena região ao redor do centro da figura diminui.

Passo 3

Letra b)

Usando os mesmos gráficos do item anterior, observa-se o seguinte:

Para n = 1 , a função de onda é mais concentrada no meio da figura e próximo da parede ela é bem pequena, enquanto para n = 2 temos dois máximos mais próximos das paredes, e a função de onda se concentra mais nesses dois máximos.

Como eles são mais próximos das paredes, ψ 2 cresce mais rápido próximo das paredes neste caso e por isso a probabilidade de achar o elétron em uma pequena região próxima da parede será maior.

Resposta

Letra a)

A probabilidade de encontrar o elétron em uma pequena região no centro do poço diminui.

Letra b)

A probabilidade de encontrar o elétron em uma pequena região próxima das paredes aumenta.

Exercício Resolvido #2

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 241-13.

Um elétron está confinado em um poço de potencial infinito unidimensional com 100   p m de largura; o elétron se encontra no estado fundamental.

Qual é a probabilidade de que o elétron seja detectado em uma região de largura Δ x = 5,0   p m em torno do ponto:

  1. x = 25   p m
  2. x = 50   p m
  3. x = 90   p m

(Sugestão: A largura Δ x é tão pequena que a densidade de probabilidade pode ser considerada constante em seu interior)

Passo 1

A probabilidade de se encontrar o elétron numa dada região a , b é dada por:

P = ∫ a b ψ 2 x d x

Mas, usando a sugestão do problema, podemos aproximá-la por:

P ≅ ψ 2 x ∙ Δ x

Onde, no caso da partícula confinada num poço unidimensional:

ψ 2 x = 2 L ∙ sen 2 ⁡ n π L ∙ x

E para o estado fundamental n = 1 .

Passo 2

Letra a)

Pelo enunciado, L = 100   p m .

Para x = 25   p m , temos:

ψ 2 x = 2 L ∙ sen 2 ⁡ π L ∙ x = 2 100 ∙ sen 2 ⁡ π 100 ∙ 25 = 2 100 ∙ sen 2 ⁡ π 4

ψ 2 = 2 100 ∙ 2 2 2 = 1 50 ∙ 2 4 = 1 100

Como Δ x = 5   p m , a probabilidade usando nossa aproximação será:

P = 5 100 = 0,05 = 5 %

Passo 3

Letra b)

Para x = 50   p m , temos:

ψ 2 x = 2 L ∙ sen 2 ⁡ π L ∙ x = 2 100 ∙ sen 2 ⁡ π 100 ∙ 50 = 2 100 ∙ sen 2 ⁡ π 2

ψ 2 = 2 100 ∙ 1 2 = 1 50

Com Δ x = 5   p m a probabilidade fica:

P = 5 50 = 1 10 = 0,1 = 10 %

Passo 4

Letra c)

Para x = 90   p m , temos:

ψ 2 x = 2 L ∙ sen 2 ⁡ π L ∙ x = 2 100 ∙ sen 2 ⁡ π 100 ∙ 90 = 2 100 ∙ sen 2 ⁡ 9 π 10

ψ 2 ≅ 0,00191

Com Δ x = 5   p m a probabilidade fica:

P ≅ 0,00191 ∙ 5 ≅ 0,00955 = 0,955 %

Resposta

Letra a)

P = 0,05 = 5 %

Letra b)

P = 0,1 = 10 %

Letra c)]

P ≅ 0,00955 = 0,955 %

Exercício Resolvido #3

UFRJ, Física 4, Prova 2, 2012.1.

Um elétron encontra-se aprisionado num poço de potencial unidimensional infinito de comprimento L (caixa quântica).

Este elétron comporta-se como uma corda presa nas extremidades ( x = 0 e x = L ) e está inicialmente no estado fundamental.

Dados m e , L , h e ∫ sen 2 ⁡ x d x = x 2 - sen ⁡ 2 x 4 , em função dos dados:

  1. Deduza a energia e o momento do elétron.
  2. Encontre o vetor de estado (função de onda) para o estado fundamental, normalizado.
  3. Qual a probabilidade de encontrar o elétron entre x = 0 e x = L / 4 , se ele estiver no segundo estado?
  4. Se o elétron estiver no quarto estado, quais os pontos de menor probabilidade de encontrar o elétron, em função de L ?
  5. Se o elétron estiver no quarto estado, quais os pontos de maior probabilidade de encontrar o elétron, em função de L ?

Passo 1

a) Deduza a energia e o momento do elétron.

Para uma onda estacionária, podemos dizer que:

L = n λ 2 → λ = 2 L n

O momento do elétron é dado por:

p n = h λ = n h 2 L

Como o elétron se encontra no estado fundamental, n = 1 , logo:

p 1 = h 2 L

Passo 2

A energia do elétron é dada por:

E 1 = p 1 2 2 m e

Substituindo a expressão para p 1 que acabamos de encontrar:

E 1 = h 2 8 m e L 2

Passo 3

b) Encontre o vetor de estado (função de onda) para o estado fundamental, normalizado.

A expressão geral para a função de onda em um problema de poço de potencial infinito é:

ψ n = A sen ⁡ n π x L

O valor de A é encontrado a partir da condição de normalização, dada por:

∫ - ∞ ∞ ψ x 2 d x = 1

Mas como o elétron está aprisionado na caixa de comprimento L , a função de onda só existe no intervalo 0 < x < L , os limites de integração serão 0 e L .

A 2 ∫ 0 L sen 2 ⁡ n π x L d x = 1

Para resolvermos essa integral, podemos fazer a seguinte substituição:

t = n π x L

d t = n π L d x

0 < x < L

0 < t < n π

Substituindo na integral, teremos:

A 2 L n π ∫ 0 n π sen 2 ⁡ t d t = 1

Segundo o enunciado:

∫ sen 2 ⁡ x d x = x 2 - sen ⁡ 2 x 4

Logo:

A 2 L n π   t 2 - sen ⁡ 2 t 4 0 n π = 1

A 2 L n π n π 2 = 1

A 2 L 2 = 1

A = 2 / L  

Substituindo na expressão da função de onda:

ψ n = 2 / L   sen ⁡ n π x L

No estado fundamental, n = 1 , logo:

ψ 1 = 2 / L   sen ⁡ π x L

Passo 4

c) Qual a probabilidade de encontrar o elétron entre x = 0 e x = L / 4 , se ele estiver no segundo estado?

Se o elétron estiver no segundo estado, então n = 2 , e a função de onda é dada por:

ψ 2 = 2 / L   sen ⁡ 2 π x L

A probabilidade de o elétron estar na região 0 ≤ x ≤ L / 4 é dada por:

p = ∫ 0 L / 4 ψ x 2 d x

Logo:

p = 2 L ∫ 0 L / 4 sen 2 ⁡ 2 π x L d x

Para resolvermos essa integral, podemos fazer a seguinte substituição:

t = 2 π x L

d t = 2 π L d x

0 < x < L / 4

0 < t < π / 2

Substituindo na integral, teremos:

p = 2 L L 2 π   ∫ 0 π / 2 sen 2 ⁡ t d t = 1 π ∫ 0 π / 2 sen 2 ⁡ t d t

Segundo o enunciado:

∫ sen 2 ⁡ x d x = x 2 - sen ⁡ 2 x 4

Logo:

p = 1 π   t 2 - sen ⁡ 2 t 4 0 π / 2

p = 1 π   π 4 = 1 4

Passo 5

d) Se o elétron estiver no quarto estado, quais os pontos de menor probabilidade de encontrar o elétron, em função de L ?

A probabilidade de encontrarmos o elétron em um determinado intervalo a < x < b é dado por:

p = ∫ a b ψ x 2   d x

Se o elétron estiver no quarto estado, então n = 4 , e a função de onda é dada por:

ψ 4 = 2 / L   sen ⁡ 4 π x L

Os pontos de menor probabilidade de encontrarmos o elétron serão os pontos onde: ψ 4 = 0

Logo:

sen ⁡ 4 π x L = 0

Isso só é possível quando o argumento da função seno é igual a um número inteiro de π :

4 π x L = n π

x = n L 4

0 < x < L

Logo, os pontos possíveis serão:

x = 0 , L 4 , L 2 , 3 L 4 ,   L

Passo 6

e) Se o elétron estiver no quarto estado, quais os pontos de maior probabilidade de encontrar o elétron, em função de L ?

A probabilidade de encontrarmos o elétron em um determinado intervalo a < x < b é dado por:

p = ∫ a b ψ x 2   d x

Se o elétron estiver no quarto estado, então n = 4 , e a função de onda é dada por:

ψ 4 = 2 / L   sen ⁡ 4 π x L

Os pontos de maior probabilidade de encontrarmos o elétron serão os pontos onde ψ 4 é máximo ou mínimo, garantindo que ψ 4 2 seja máximo. Logo:

sen ⁡ 4 π x L = ± 1

Isso só é possível quando:

4 π x L = 1 2 + n π

x = 1 2 + n L 4

0 < x < L

Logo, os pontos possíveis serão:

x = L 8 , 3 L 8 , 5 L 8 , 7 L 8

Resposta

a)

p 1 = h 2 L

E 1 = h 2 8 m e L 2

b)

ψ 1 = 2 / L   sen ⁡ π x L

c)

p = 1 4

d)

x = 0 , L 4 , L 2 , 3 L 4 ,   L

e)

x = L 8 , 3 L 8 , 5 L 8 , 7 L 8

Exercício Resolvido #4

Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 240-4, modificado

Um próton é confinado em um poço de potencial infinito unidimensional com 100   p m de largura.

Qual é a energia do estado fundamental?

Dado:

Massa do próton m p = 1,673 ∙ 10 - 27   k g

Passo 1

A energia de uma partícula confinada em um poço de potencial infinito unidimensional é:

E n = h 2 8 m L 2 n 2

Para uma partícula no estado fundamental temos n = 1 , e a energia fica:

E = h 2 8 m L 2

Passo 2

Temos que:

  • Constante de Planck h = 6,626 ∙ 10 - 34   J ∙ s
  • Massa do próton m p = 1,673 ∙ 10 - 27   k g
  • Largura do poço L = 100   p m = 100 ∙ 10 - 12   m

Substituindo:

E = 6,626 2 ∙ 10 - 68 8 ∙ 1,673 ∙ 10 - 27 ∙ 10 - 20 ≅ 3,28 ∙ 10 - 21   J

Passando para elétrons-Volt, temos:

1   e V = 1,602 ∙ 10 - 19   J

E = 3,28 ∙ 10 - 21 1,602 ∙ 10 - 19 = 2,05 ∙ 10 - 2   e V = 0,0205   e V

Resposta

E = 3,28 ∙ 10 - 21   J = 0,0205   e V

Exercício Resolvido #5

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 260-40.5

É necessário fornecer 3,0   e V de energia a um átomo para excitar um elétron do nível fundamental até o primeiro nível excitado.

Considere o átomo um elétron em uma caixa e calcule a largura L da caixa.

Dado:

Massa do elétron m e = 9,1 ∙ 10 - 31   k g

Passo 1

O que o problema nos diz é que a diferença de energia entre o estado fundamental e o primeiro nível excitado ( E 2 - E 1 ) é 3,0   e V .

A energia em qualquer nível é dada por:

E n = n 2 E 1

Onde E 1 é a energia no estado fundamental, dada por:

E 1 = h 2 8 m L 2

Passo 2

Δ E = E 2 - E 1 = 2 2 - 1 2 h 2 8 m L 2

Rearrumando:

L 2 = 3 h 2 8 m Δ E

Onde:

h = 6,626 ∙ 10 - 34   J   s ;

Δ E = 3,0   e V = 4,8 ∙ 10 - 19   J ;

m = 9,1 ∙ 10 - 31   k g ;

Logo:

L = h 3 8 m Δ E

L = 6,626 ∙ 10 - 34 3 8 ∙ 9,1 ∙ 10 - 31 ∙ 4,8 ∙ 10 - 19

L = 6,13 ∙ 10 - 10   m

L = 0,61   n m

Resposta

0,61   n m

Exercício Resolvido #6

UFRJ, Física 4, Prova 2, 2011.2

Uma partícula de massa m está confinada em um tubo de comprimento L .

O momento linear e a energia dessa partícula são respectivamente iguais a:

  1. n h / L ; n 2 h 2 / ( 8 L 2 m ) ,   n = 1 ,   2 , …
  2. n h / L ; n 2 h 2 / ( 8 L 2 m ) ,   n = 0 ,   1 ,   2 , …
  3. n h / ( 2 L ) ; n 2 h 2 / ( 8 L 2 m ) ,   n = 1 ,   2 , …
  4. n h / ( 2 L ) ; n 2 h 2 / ( 8 L 2 m ) ,   n = 0 ,   1 ,   2 , …
  5. n h / ( 2 L ) ; n 2 h 2 / ( 4 L 2 m ) ,   n = 1 ,   2 , …
  6. n h / ( 2 L ) ; n 2 h 2 / ( 4 L 2 m ) ,   n = 0 ,   1 ,   2 , …
  7. 2 L / ( n h ) ; n 2 h 2 / ( L 2 m ) ,   n = 1 ,   2 , …
  8. 2 L / n h ; 2 L 2 / ( n 2 h 2 m ) ,   n = 0 ,   1 ,   2 , …
  9. 2 L / n h ; 2 L 2 / ( n 2 h 2 m ) ,   n = 1 ,   2 , …
  10. L / ( n h ) ; L 2 / ( 2 n 2 h 2 m ) ,   n = 0 ,   1 ,   2 , …
  11. L / ( n h ) ; L 2 / ( 2 n 2 h 2 m ) ,   n = 1 ,   2 , …
  12. n h / L ; n 2 h 2 / ( L 2 m ) ,   n = 0 ,   1 ,   2 , …

Passo 1

Uma vez que a partícula está confinada no tubo, podemos tratar o problema como um poço de potencial infinito.

Assim, a energia da partícula é dada por:

E = n 2 h 2 8 m L 2

Podemos relacionar a energia e o momento linear o elétron a partir de:

E = p 2 2 m

p = 2 m E

p = 2 m n 2 h 2 8 m L 2 = n 2 h 2 4 L 2

p = n h 2 L

No estado mais baixo de energia ( estado fundamental) n não pode ser igual a zero pois, neste caso, a função de onda seria sempre zero (a energia do elétron nunca é nula).

Assim, os valores possíveis para n são:

n = 1 ,   2 ,   …

Resposta

Letra (c): n h / ( 2 L ) ; n 2 h 2 / ( 8 L 2 m ) ,   n = 1 ,   2 , …

Exercício Resolvido #7

UFRJ, Física 4, Prova 2, 2014.1

Seja Δ E n a diferença de energia entre dois níveis de energia adjacentes E n e E n + 1 para uma partícula em uma caixa (poço infinito). A razão R n = Δ E n / E n compara a energia de um nível com a diferença de energia entre este nível de energia e a energia de um nível adjacente.

Qual é o valor máximo de R n ?

a ) 3

b ) 5

c ) 1

d ) 5 2

e ) 1 2

f ) 3 2

g ) Nenhuma das anteriores.

Passo 1

As energias permitidas em um poço de potencial infinito são dadas por:

E n = n 2 E 1

Onde n representa o nível de energia e E 1 representa a energia no estado fundamental, dada por:

E 1 = h 2 8 m L 2

Passo 2

Substituindo as expressões do Passo 1 na expressão de R n , teremos:

R n = Δ E n E n

R n = E n + 1 - E n E n

R n = n + 1 2 E 1 - n 2 E 1 n 2 E 1 = E 1 n + 1 2 - n 2 n 2 E 1

Beleza, agora é só ir dando uma arrumada na casa.

R n = n + 1 2 - n 2 n 2

R n = n 2 + 2 n + 1 - n 2 n 2

R n = 2 n + 1 n 2

R n = 2 n + 1 n 2

Passo 3

Analisando a expressão de R n podemos ver que, quanto maior o valor de n , menor será o valor de R n . Assim, para que R n tenha o maior valor possível, n deverá ter o menor valor possível, logo:

n = 1

R 1 = 2 + 1

R 1 = 3

Assim, a resposta certa é a letra a .

Resposta

a ) 3

Exercício Resolvido #8

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 260-40.1

  1. Determine o nível de energia mais baixo para a partícula em uma caixa supondo que a partícula seja uma bola de bilhar m = 0,20   k g e que a largura da caixa seja 1,5   m , o tamanho de uma mesa do jogo de bilhar. (Suponha que a bola de bilhar deslize sem atrito em vez de rolar. Ou seja, despreze a energia cinética da rotação.).
  2. Como a energia do item (a) é totalmente dada pela energia cinética, a que velocidade isso corresponde? Com essa velocidade, quanto tempo a bola levaria para ir de uma extremidade da mesa até a outra?
  3. Qual é a diferença de energia entre os níveis n = 2 e n = 1 ?
  4. Os efeitos da mecânica quântica são importantes para o jogo de bilhar?

Passo 1

Letra (a): Determine o nível de energia mais baixo para a partícula em uma caixa supondo que a partícula seja uma bola de bilhar m = 0,20   k g e que a largura da caixa seja 1,5   m , o tamanho de uma mesa do jogo de bilhar. (Suponha que a bola de bilhar deslize sem atrito em vez de rolar. Ou seja, despreze a energia cinética da rotação.).

O nível mais baixo de energia corresponde à energia do estado fundamental, dada por:

E 1 = h 2 8 m L 2

Onde:

h = 6,626 ∙ 10 - 34   J   s ;

m = 0,2   k g ;

L = 1,5   m ;

Logo:

E 1 = 6,626 ∙ 10 - 34 2 8 ∙ 0,2 ∙ 1,5 2 = 1,22 ∙ 10 - 67   J

Passo 2

Letra (b): Como a energia do item (a) é totalmente dada pela energia cinética, a que velocidade isso corresponde? Com essa velocidade, quanto tempo a bola levaria para ir de uma extremidade da mesa até a outra?

Comparando a energia encontrada no item (a) com a energia cinética, temos:

m v 2 2 = E 1

v = 2 E 1 m

Onde:

m = 0,2   k g ;

E 1 = 1,22 ∙ 10 - 67   J ;

Logo:

v = 2 ∙ 1,22 ∙ 10 - 67 0,2 = 1,1 ∙ 10 - 33   m / s

Passo 3

O tempo necessário para chegar ao outro lado da caixa é dado por:

v = Δ s Δ t → Δ t = Δ s v = L v

Δ t = 1,5 1,1 ∙ 10 - 33 = 1,4 ∙ 10 33   s  

Passo 4

Letra (c): Qual é a diferença de energia entre os níveis n = 2 e n = 1 ?

A energia em qualquer nível de energia é dado por:

E n = n 2 E 1

Logo:

E 2 - E 1 = 2 2 - 1 2 E 1

Onde E 1 = 1,22 ∙ 10 - 67   J .

E 2 - E 1 = 3 ∙ 1,22 ∙ 10 - 67 = 3,66 ∙ 10 - 67   J

Passo 5

Letra (d): Os efeitos da mecânica quântica são importantes para o jogo de bilhar?

Não, pois a energia no estado fundamental é muito pequena para uma massa relativamente grande.

Além disso, a velocidade é muito pequena em comparação com a escala da bola, que fica com um tempo de percurso correspondente a mais de um bilhão de anos.

Resposta

Letra (a):

E 1 = 1,22 ∙ 10 - 67   J

Letra (b):

v = 1,1 ∙ 10 - 33   m / s

Δ t = 1,4 ∙ 10 33   s  

Letra (c):

E 2 - E 1 = 3,66 ∙ 10 - 67   J

Letra (d):

Não, pois a energia no estado fundamental é muito pequena para uma massa relativamente grande.

Exercícios de Livros Relacionados

Uma partícula está no primeiro estado excitado (n = 2) de uma caixa unidimensional com comprimento L. (A caixa tem uma extremidade na origem e a outra extremidade no eixo x positivo.) Encontre (a) x e
Uma caixa unidimensional está no eixo x na região de 0 ≤ x ≤ L. Uma partícula nesta caixa está em seu estado fundamental. Calcule a probabilidade de a partícula ser encontrada na região (a) x L21 0
Um dado de seis lados tem o número 1 pintado em três lados e o número 2 pintado nos outros três lados. (a) Qual é a probabilidade de aparecer 1 quando o dado é lançado? (b) Qual é o valor esperado do