Spin e o Princípio da Exclusão de Pauli

Mas... acho que isso não diria nada.

Essa propriedade (o spin) age como se fosse a rotação do elétron ao redor do próprio eixo. Ele tem tudo igual a uma rotação. Assim como a rotação ao redor do núcleo, que é descrita pelos números quânticos e , ele é descrito por dois números quânticos e .

O módulo do spin do elétron e sua componente ao longo de um “eixo ” seguem a mesma forma do momento angular:

Sendo que eu posso ter

Mas para o elétron eu tenho SEMPRE.

Todas as partículas (elétron, nêutron, próton, fóton, ...) podem ter o número de spin como sendo uma fração ou um número inteiro, mas esse número não muda! Qualquer elétron tem spin , em qualquer caso. Assim como qualquer fóton tem sempre.

Por isso, os valores de possíveis são:

Que chamamos de spin down e spin up. Em geral, representamos um por uma setinha pra cima e outro por uma setinha pra baixo.

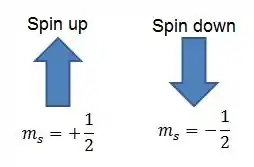
Esse número de spin é uma propriedade da partícula que age exatamente como se fosse uma rotação, e por isso eu disse pra você que “é como se fosse a rotação ao redor do próprio eixo”. Seria como se todas as partículas sempre andassem por aí dando rodopios.

Mas na verdade, ninguém passa todo dia, o dia todo, andando nas ruas e dando rodopios que nem bailarinas ou bailarinos em um show.

Essa é uma “propriedade” do elétron ( de certa forma como a massa ou a carga dele). Comparar com os rodopios facilita, mas o elétron NÃO está girando ao redor do próprio eixo!

O princípio da exclusão de Pauli

O princípio da exclusão de Pauli nos diz que dois elétrons diferentes não podem ter, ao mesmo tempo, todos os seus números quânticos iguais.

Se pensarmos no elétron no hidrogênio, isso significa que apenas um poderá ser o detentor do título de . Mas e o ? Bem, o de todos é igual.

Vou tentar usar o átomo de Alumínio, que tem elétrons, pra explicar o que eu quero dizer. Vamos desprezar a interação entre os elétrons, e considerar que todos os níveis são iguais aos do hidrogênio.

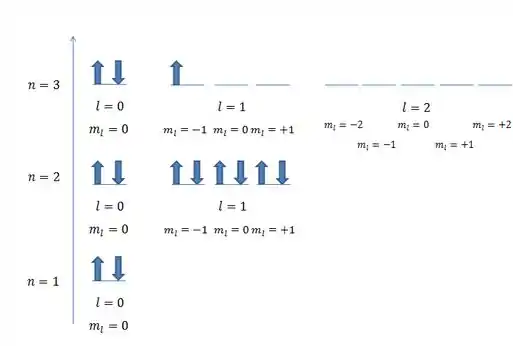
Lembrando das restrições:

Temos que ir começando de baixo pra cima, pra garantir a menor energia (estado fundamental).

Assim, primeiro eu coloquei dois elétrons em .

Para , eu posso ter ou . No caso de , como eu tenho , só posso colocar dois elétrons (spin up e spin down).

Porém, quando , eu posso ter ! Para cada um desses casos, eu tenho duas setinhas!

É como se cada estado fosse uma casinha dos elétrons. A casinha é dada por uma trinca de números e em cada casinha, eu só posso ter dois elétrons, um virado pra cima (spin up), e um pra baixo (spin down).

Eu nunca disse que a casinha era grande.

Esse princípio funciona para mais do que só um átomo. Sempre que eu tiver elétrons com um conjunto de números quânticos quaisquer, ele vai valer. A única coisa que não muda é o spin do elétron.

Por exemplo, no caso do poço infinito, os elétrons só tem o número quântico (além do spin). Logo, para cada , eu só tenho dois elétrons.

Agora, vamos fazer um exercício, pra fixar essa idéia.