Efeito Doppler Transversal
Teoria
O drama agora é o seguinte: ao invés da fonte se mover ao longo da linha que a liga com o detector, como vimos anteriormente, agora a fonte se move na direção transversal.
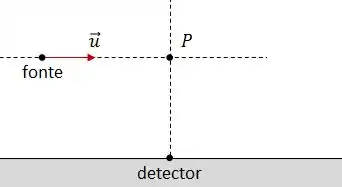
Quando a fonte passa pelo ponto , a sua velocidade é perpendicular à linha que a liga ao detector. Nesse exato instante, a fonte não está se aproximando e nem se afastando do detector.
No entanto, se a fonte está emitindo ondas luminosas, haverá um efeito Doppler, chamado de efeito Doppler Transversal.
Nesse caso, a frequência medida pelo detector será dada por:
Onde é a frequência própria da fonte.
Efeito Doppler transversal para baixas velocidades
No caso em que , a frequência medida pelo detector pode ser dada por:
Show! Vamos ao exercício.
Efeito Doppler transversal para baixas velocidades
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 180-38.
Uma lâmpada de sódio está se movendo em círculos em um plano horizontal com uma velocidade constante de , enquanto emite luz com um comprimento de onda próprio .
Um detector situado no centro de rotação da lâmpada é usado para medir o comprimento de onda da luz emitida pela lâmpada, e o resultado é .
Qual é o valor da diferença ?
Passo 1
Nesse caso, a frequência medida pelo detector é dada por:
Utilizando a expressão , teremos:
Dividindo os dois lados por , teremos:
Passo 2
A diferença entre os comprimentos de onda será:
Onde:
Logo: