Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Movimento de Foguetes

Ver Todos os Exercícios

Teoria

A NASA vai lançar essa semana o foguete “BIRL 1” ,que tem massa m i quando sai da sua base lá em Houston.

Mas pensa aí! Quando o foguete vai subindo, vai gastando combustível e a sua massa vai diminuindo, certo? Se não houver a resistência do ar, teremos conservação do momento linear desse sistema aí. Mas pera, como que eu relaciono a velocidade final e inicial?

Inicialmente o nosso foguete tem uma massa m e uma velocidade v no espaço.

Ele joga para trás uma massa de gás d m , com uma velocidade relativa ao foguete - v e , que chamamos de velocidade de escape. Num referencial de fora a velocidade desse gás será v - v e . O foguete agora tem massa m - d m e velocidade v + d v

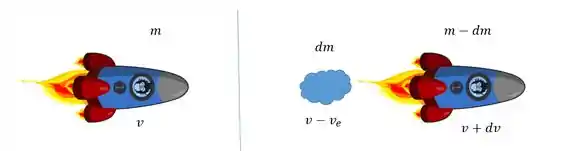
Pela conservação de momento

m v = d m v - v e + m - d m v + d v

m v = d m v - d m v e + m v + m d v - d m v - d m d v

0 = - d m v e + m d v - d m d v

O produto d m d v é o produto de duas coisas muito pequeninas assim podemos desprezá-lo

m d v = v e d m

d m é a massa de gás expelida e - d m é o quanto de massa o foguete perdeu, assim para o foguete fica

m d v = - v e d m

Dividindo tudo por d t

m d v d t = - v e d m d t

Que é tipo uma segunda lei. Como o foguete perde massa, d m d t é negativo e o lado direito da equação e positivo o que faz com que o foguete ganhe velocidade!

Se quiséssemos adicionar uma força externa, como a gravitacional por exemplo basta fazer

m d v d t = - v e d m d t + F e x t

Voltando a m d v = - v e d m

Se o foguete tem velocidade inicial v 0 e massa inicial m 0 e no instante t , massa m ( t ) e velocidade v ( t ) .

m d v = - v e d m → ∫ v 0 v t d v = - v e ∫ m 0 m t d m m

v t - v 0 = - v e ln ⁡ m t m 0

m ( t ) será sempre menor ou igual a m 0 , isso quer dizer que v t - v 0 ≥ 0 , ou seja, v t ≥ v 0 .

Meio maluco? Sim, mas é tranquilão de lidar com essa formulinha. Vamos exercitar. ;D

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

A hidrazina é uma substância altamente instável. Essa instabilidade pode gerar grandes explosões, sendoa hidrazina perfeito para propulsão de foguetes e satélites. Um foguete,que possui 1 milhão de kilogramas de hidrazina, será lançado em 15 de setembro do ano que vem e o engenheiro espacial responsável pela missão espacial deve projetar um motor que tenha propulsão necessária para que o foguete atinja uma velocidade de 1 k m / s ao chegar na extratosfera. Qual a velocidade de propulsão v e de hidrazina do para que ele consiga obter o seu feito com exatamente 400mil kilogramas de hidrazina? Lembrando que a massa da carcaça do foguete é de 200mil kilogramas .

Passo 1

Temos a nossa querida formulinha dada por:

Δ v = v e . ln ⁡ m i m f  

Aplicando os valores aqui, teremos:

1000 m s = v e . ln ⁡ 1000 + 200 400 + 200   = l n 2 . v e

v e = 1000 l n 2 m / s ≅ 1442,69   m / s

Resposta

v e = 1442,69 m / s  

Exercício Resolvido #2

Elaboração Própria

Um foguete,que possui 1 milhão de kilogramas de hidrazina, será lançado em breve e o engenheiro aeroespacial responsável pela missão espacial deve projetar um motor que tenha propulsão necessária para que o foguete atinja uma velocidade de 1 k m / s ao chegar na extratosfera. Além disso, velocidade de propulsão máxima do foguete é de 2 k m / s . Qual a massa de combustível final no foguete quando ele estiver a passar na extratosfera? Lembrando que a massa da carcaça do foguete é de 200mil kilogramas .

Passo 1

Temos a nossa querida formulinha dada por:

Δ v = v e . ln ⁡ m i m f  

Aplicando os valores aqui, teremos:

1000 = 2000 . ln ⁡ 1000 + 200 m c + 200  

Passo 2

1 2 = ln ⁡ 1200 m c + 200  

Mexendo um pouquinho com isso aqui, vamos encontrar:

e 1 2 = 1200 m c + 200

m c + 200 = 1200 e 1 2

m C = 527,8367   m i l     k i l o g r a m a s

Resposta

m C = 527,8367   m i l     k i l o g r a m a s

Exercícios de Livros Relacionados

Uma sonda espacial de 6090k g , movendo-se com o nariz à frente em direção a Júpiter a uma velocidade de 105m / s em relação ao Sol, aciona o motor, ejetando 80,0k g de produtos de combustão a uma vel
Um foguete tem massa total M i=360k g , incluindo M f=330k g de combustível e oxidante. No espaço interestelar, ele parte do repouso na posição x=0 , liga o motor no instante t=0 e expele gases de exa
Na Seção 8.6 consideramos um foguete disparado no espaço sideral, onde não existe gravidade nem resistência do ar. Suponha agora que o foguete esteja sendo acelerado verticalmente a partir da superfíc
Utilizando os dados da tabela da pg.164, calcule, para o 3 ° . Estágio do sistema Saturno V-Apolo.a) a velocidade de escape dos gases da combustão; b) o incremento de velocidade produzido por este est
Considere um foguete lançado verticalmente, e leve em conta o efeito da gravidade sobre seu movimento. Escreva a equação de movimento (generalização da Equação 7.20) para o foguete.