Teoria
O diagrama T x S é um diagrama onde o eixo vertical representa a temperatura e o eixo horizontal a entropia. Bora conhecer mais dele?!
📢 Clique para ver mais:
- Ciclo de Carnot
- Máquinas Térmicas
- Primeira Lei da Termodinâmica
- Variação de Entropia de um Gás Ideal
Diagrama TS para o Processo Adiabático
Em um processo adiabático não temos troca de calor com o ambiente externo e a variação de entropia é igual a zero.
Se a variação de entropia é igual a zero, então a entropia é constante! Se
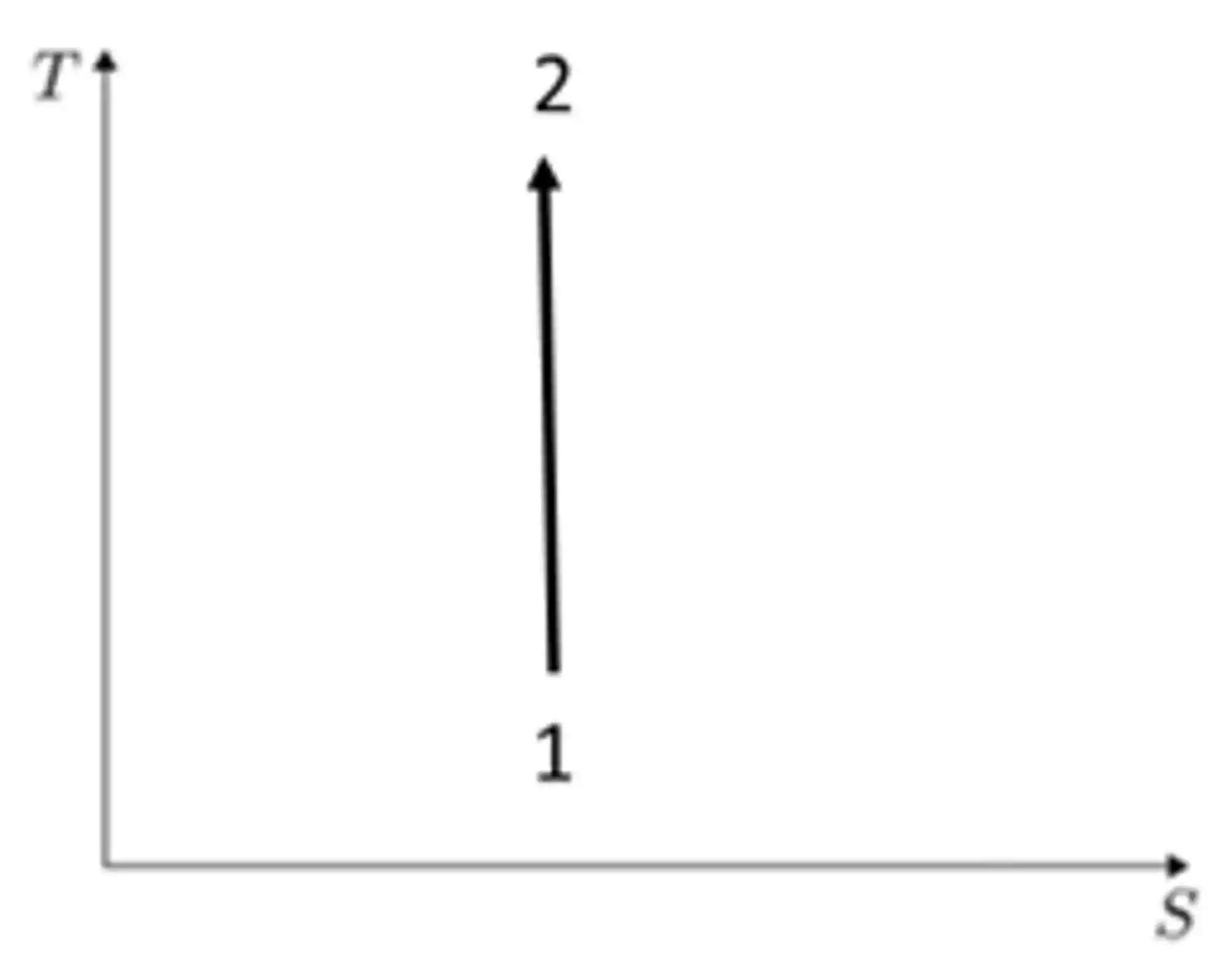
Se a a variação de temperatura foi maior que zero, então o sentido se inverteria
Você também pode conferir esse conteúdo em vídeo:
Diagrama TS para o Processo Isotérmico
Em um processo isotérmico a variação de entropia é dada por:
Podemos representar uma transformação isotérmica em um diagrama TS da seguinte forma:
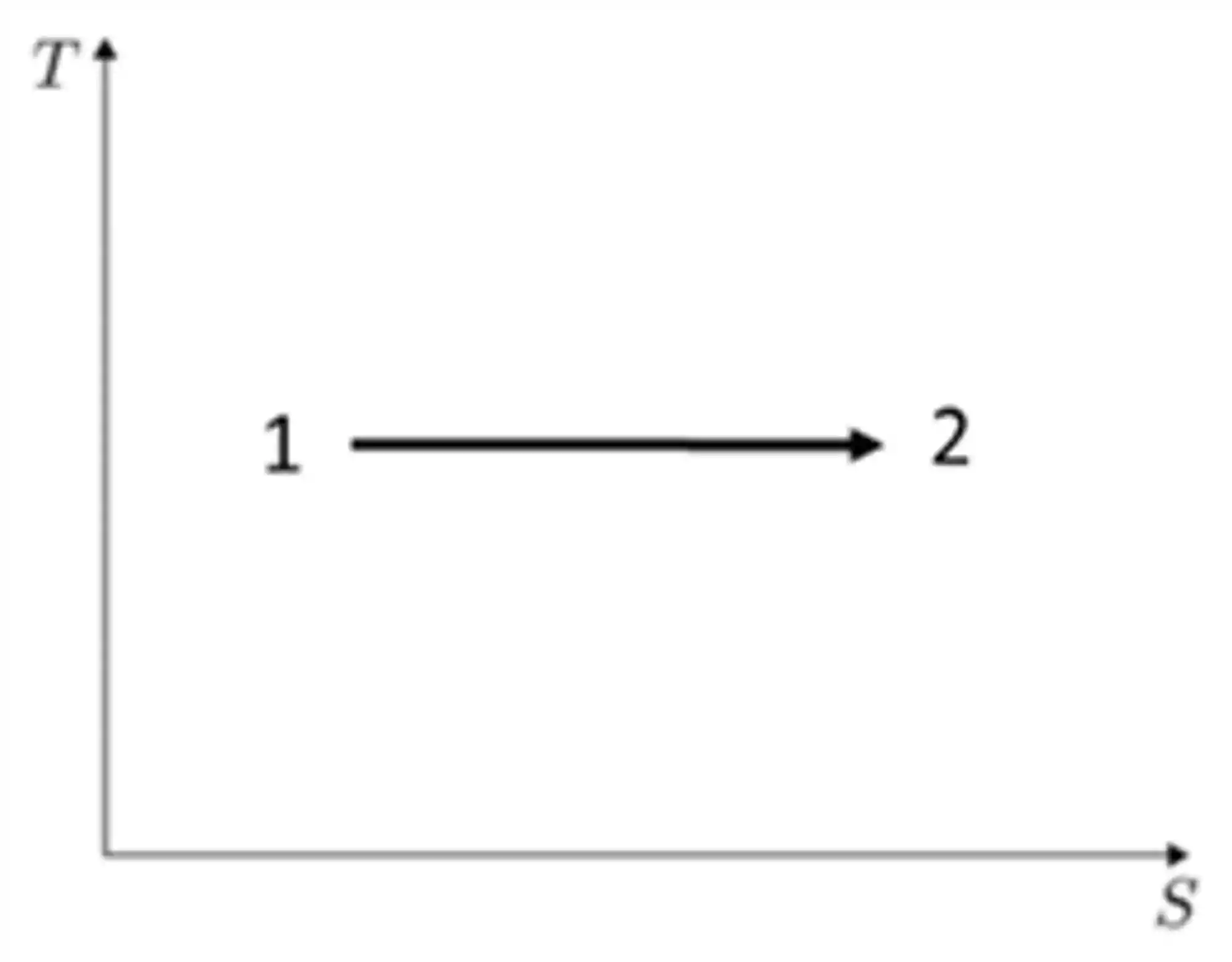
Se a variação de volume for positiva, então
Diagrama TS para o Processo Isobárico
A variação de entropia em um processo isobárico pode ser escrito da seguinte forma:
Se quisermos escrever a temperatura em função da entropia:
Quando plotamos o diagrama TS ficamos com:
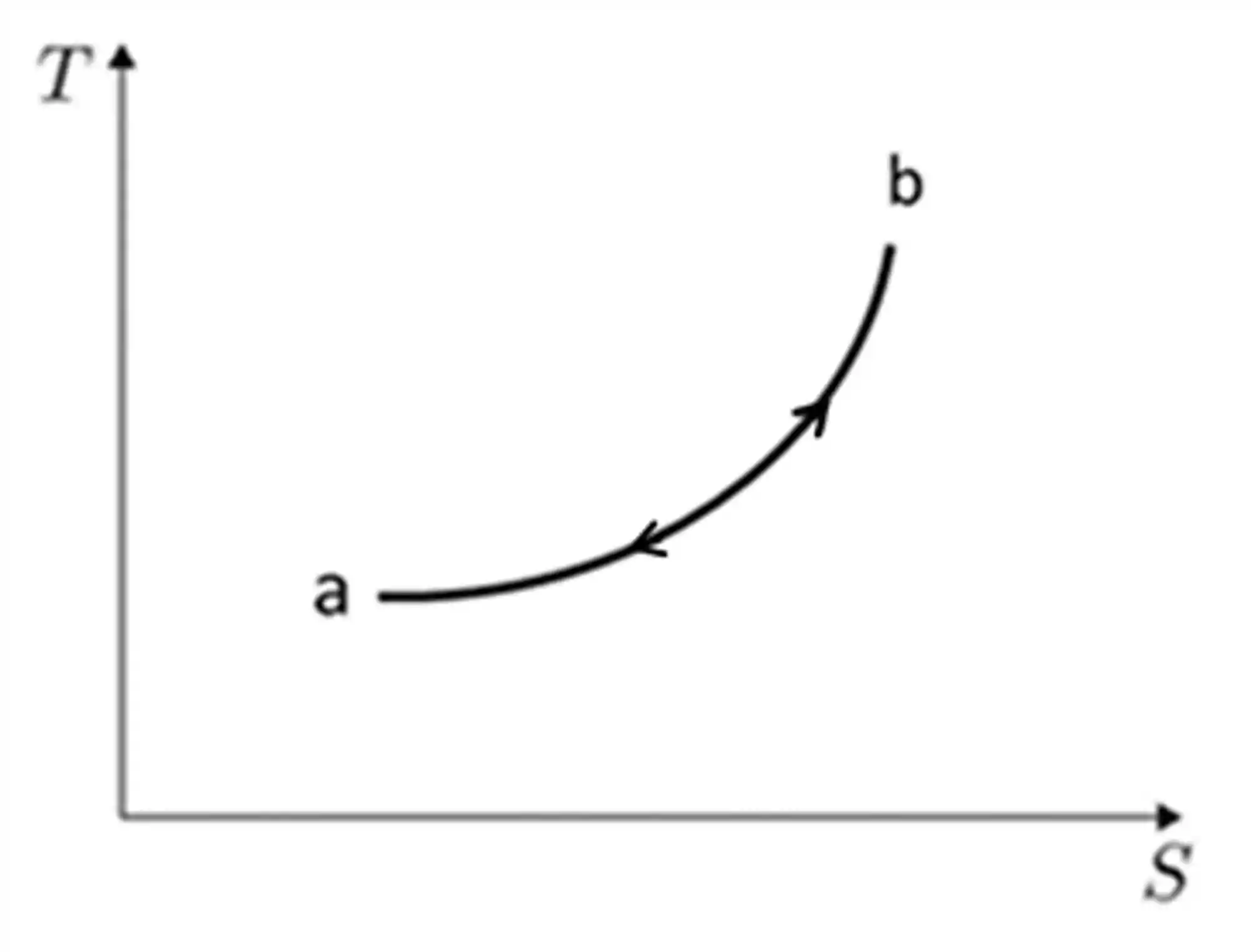
Ciclo de Carnot
O Ciclo de Carnot é um ciclo termodinâmico ideal composto por quatro transformações reversíveis, sendo duas transformações isotérmicas e duas adiabáticas alternadamente, podemos representa-lo da seguinte forma:
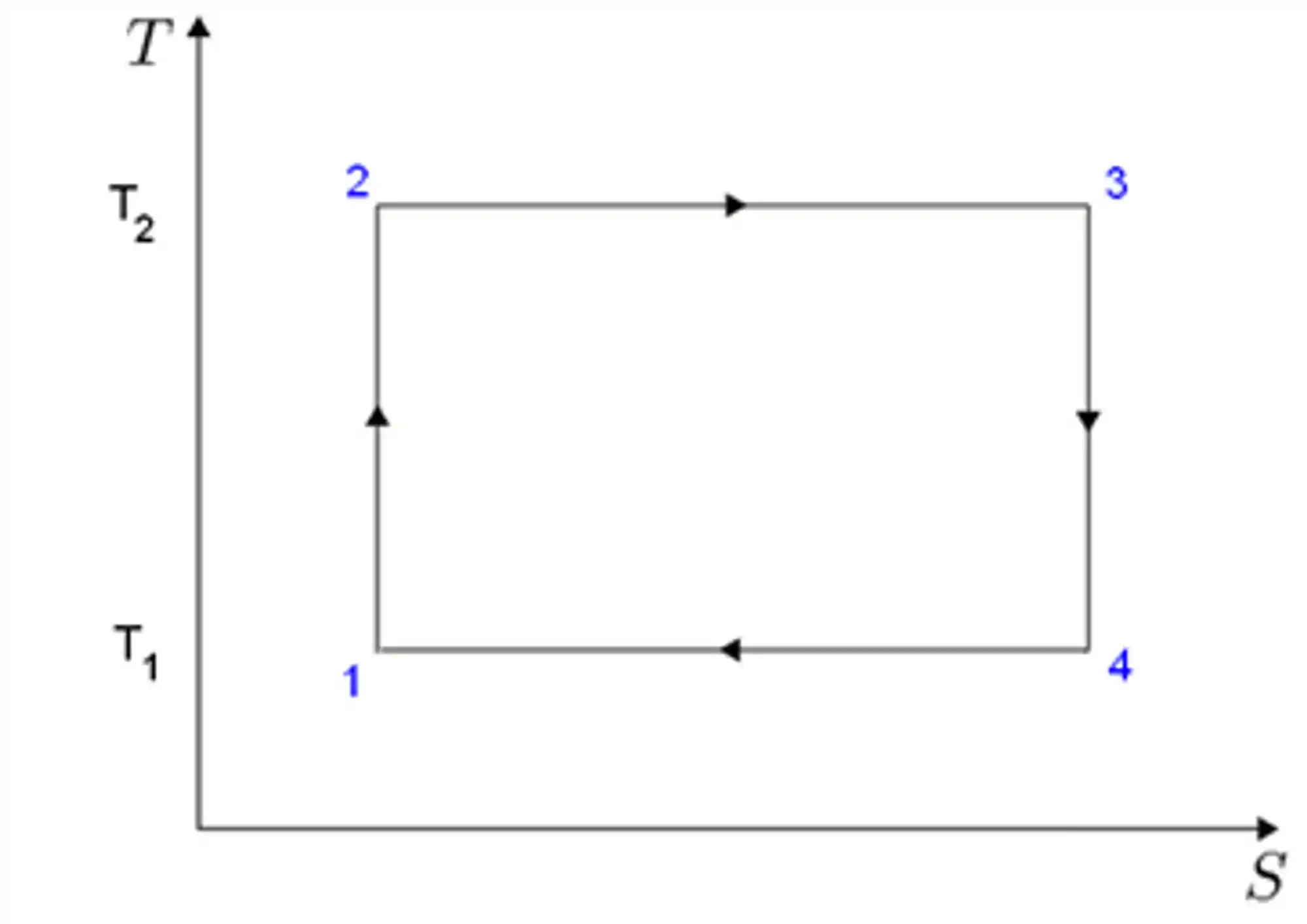
Os processos no ciclo de Carnot são:
- 1-2: compressão adiabática
- 2-3: expansão isotérmica
- 3-4: expansão adiabática
- 4-1: compressão isotérmica
Os processos 1-2 e 3-4 são adiabáticos e reversíveis (entropia constante); e os processos 2-3 e 4-1 são isotérmicos (temperatura constante).
Agora vamos praticar com exercícios?
Diagrama TS para o Processo Isotérmico
Diagrama TS para o Processo Isobárico
Ciclo de Carnot
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – 1ª Prova – 2013.2
Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISÓCORAS, como mostra o diagrama - na figura.
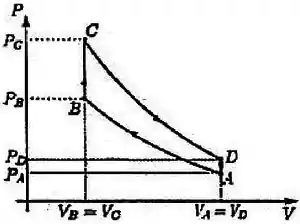
Marque a opção que melhor representa o MESMO ciclo em um diagrama -.
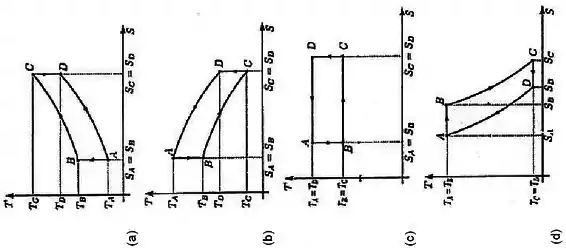
Passo 1
O primeiro passo para transformar um diagrama - em - é conferir se tem alguma isoterma ou adiabática, porque no diagrama - essas transformações são retas.
Nesse caso, temos duas transformações adiabáticas.
Pela figura, as adiabáticas são e .
Transformações adiabáticas são retas verticais no diagrama -, pois a entropia é constante.
Observação: lembrando que processos adiabáticos e reversíveis tem entropia constante:
Pelas alternativas, podemos eliminar a letra .
Passo 2
Agora que sabemos que temos duas adiabáticas, temos que ver o sentido.
Primeiro: no diagrama - mostrado, o sentido do ciclo é horário.
Como o trabalho é a área do ciclo nos dois diagramas, então o sentido do ciclo no diagrama - também deve ser horário.
Observação: lembrando que o sentido do ciclo determina se o trabalho é positivo ou negativo. Se for sentido horário, é positivo e vice-versa.
Assim, podemos eliminar as letras e .
Logo, só nos resta a letra como resposta.
Passo 3
Só para garantir que esta é a resposta certa, podemos ver que nos processos isovolumétricos, a pressão aumenta.
Aplicando a equação dos gases ideais no processo , por exemplo:
Como :
Como , então .
De fato, podemos observar isso na resposta da letra !
Resposta
Alternativa .
Exercício Resolvido #2
UFRJ – 1ª Prova – 2014.1
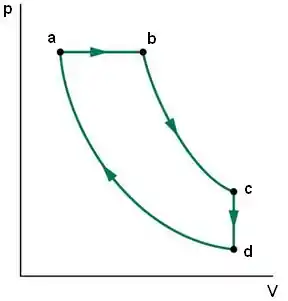
de um gás ideal é submetido a uma transformação cíclica reversível, representada no plano pelo diagrama abaixo:
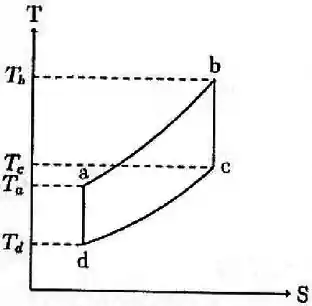
Na transformação , o gás sofre um aquecimento a pressão constante; em , um resfriamento adiabático; em , um resfriamento a volume constante; finalmente, em , um aquecimento adiabático.
Mostre, partindo de primeiros princípios, que
Dado que, no aquecimento a pressão constante, e, no resfriamento a volume constante, , calcule o trabalho realizado neste ciclo.
Desenhe o diagrama correspondente no plano , descrevendo cada processo, e calcule o trabalho, da maneira tradicional,APENAS no processo a pressão constante . Escreva o resultado em termos das temperaturas do sistema.
Passo 1
Resolvendo item
Como o ciclo é reversível, podemos calcular a variação de entropia do ciclo desta forma:
Na forma diferencial:
Substituindo na integral do ciclo:
Então, essa integral é o saldo de calor no ciclo.
Aplicando a Primeira Lei da Termodinâmica no ciclo:
Como a variação de energia interna só depende dos estados inicial e final, em um ciclo essa variação é zero.
Logo:
Então, se
Logo:
Passo 2
Resolvendo item
O trabalho realizado é dado por:
Ou seja:
Nos processos e , a área abaixo da curva é zero.
Então, precisamos calcular essa integral só nos processos e .
Passo 3
Calculando integral no processo :
Nesse processo, o enunciado nos disse que
Pois, nesse processo, a pressão é constante.
Substituindo na integral:
Logo:
Passo 4
Calculando integral no processo :
Nesse processo, o enunciado nos disse que
Pois, nesse processo, o volume é constante.
Substituindo na integral:
Logo:
Passo 5
Substituindo o que encontramos na integral do ciclo:
Logo, o trabalho realizado no ciclo é dado por:
Passo 6
Para desenhar o diagrama -, vamos ver quais curvas correspondem a cada processo:
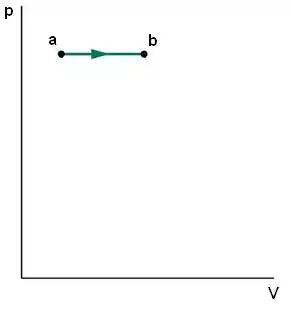
: aquecimento a pressão constante
Nesse caso, como a pressão é constante, a curva é uma reta horizontal.
Como é um aquecimento, a direção é da esquerda para a direita, pois:
Como , então .
Pela equação do gás ideal a pressão constante:
Como a temperatura aumenta, o volume também aumenta. Por isso, o sentido da seta é da esquerda para a direita.
Passo 7
: resfriamento adiabático
A curva adiabática tem direção da esquerda para a direita, pois a temperatura diminui.
Sabemos que a curva adiabática é mais inclinada do que as isotermas:
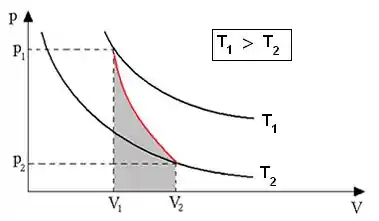
Então, nosso gráfico fica assim:
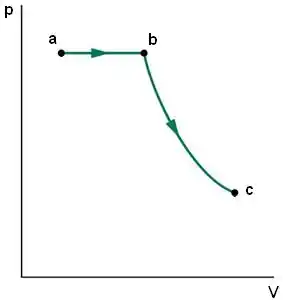
Passo 8
: resfriamento a volume constante
Nesse caso, a curva é uma reta vertical, pois o volume é constante.
Pela equação do gás ideal a volume constante:
Como a temperatura diminuiu, a pressão também diminui.
Então a direção é para baixo.
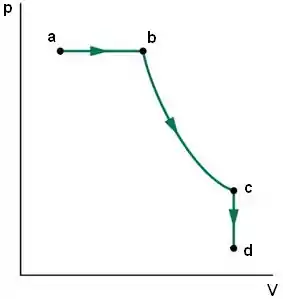
Passo 9
: aquecimento adiabático
Como é um aquecimento, a curva tem direção da direita para esquerda.
Pra fechar o ciclo, só poderia ser assim mesmo.
Então o gráfico fica assim:
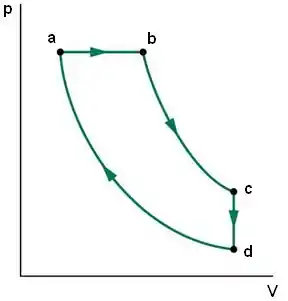
Passo 10
Eu imagino que a “maneira tradicional” de calcular trabalho é pela integral:
Ou seja, a área sobre a curva no diagrama -.
No processo isobárico , temos .
Logo:
O problema nos pede que o trabalho seja colocado em termos das temperaturas.
Colocando a equação do gás ideal nos pontos e :
Subtraindo a segunda da primeira:
Como :
Resposta
Exercício Resolvido #3
UFRJ – 1ª Prova – 2014.2
A figura mostra um processo cíclico, sofrido por moles de um gás ideal monoatômico, representado pelo plano , onde é a energia interna do sistema, e é a entropia. A respeito desse sistema, responda as seguintes questões:
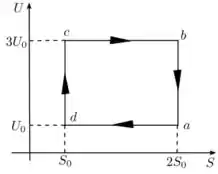
Identifique cada processo, isso é, se é isocórico, isotérmico, isobárico ou adiabático.
Calcule o trabalho realizado pelo sistema e o calor trocado por ele em cada etapa em termos de Indique explicitamente a convenção de sinais adotada.
Diga se o ciclo corresponde a uma máquina térmica ou a um refrigerador. Se for uma máquina, calcule a eficiência térmica, se for um refrigerador, calcule o coeficiente de desempenho.
O que podemos dizer desse ciclo em relação ao ciclo de Carnot? Qual é o mais eficiente?( Ou de melhor desempenho?).
Passo 1
Vamos lá:
Primeiro, de pra
Como nesse processo a energia interna é a mesma, a variação de energia interna é zero. Isso só acontece quando a temperatura é constante e, portanto, num processo isotérmico:
Isotérmico.
Nesse processo a variação de entropia é nula, então, só pode ser um processo adiabático:
adiabático.
Mesma coisa de antes, sem variação de energia interna, logo, isotérmico.
Isotérmico.
Sem variação de entropia, então, processo adiabático.
adiabático.
Passo 2
Por ser um processo isotérmico:
Usando a primeira lei:
Show?
Agora, lembrando da equação diferencial da entropia:
Como , se integrarmos nos dois lados:
Opa, encontramos uma equação para o trabalho. Só que não podemos usar esse
Lembra da equação da energia interna?:
Como o gás é monoatômico,
E:
Então:
Passo 3
Nesse caso, a variação de entropia é igual a zero por esse processo ser adiabático. Então, por ser adiabático, não há troca de calor:
Passo 4
:
Novamente, um processo isotérmico. Então vai ser bem parecido:
E:
Então:
Passo 5
:
Processo adiabático! Então:
Passo 6
Como descobrir se o ciclo representa uma máquina térmica ou um refrigerador? Bom, basta calcular o trabalho total.
Se for positivo, será uma máquina térmica, se for negativo, um refrigerador, já que a máquina térmica sempre “anda” no sentido horário e o refrigerador no sentido anti-horário. Assim:
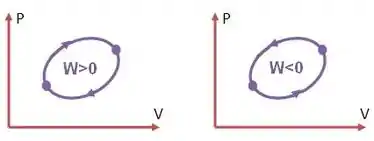
O trabalho total é a soma de todos os trabalhos e vale:
Como o trabalho total é positivo, o ciclo representa uma máquina térmica. Então o que precisamos calcular é a eficiência térmica:
Bom, o trabalho do ciclo nós já sabemos, mas quanto vale o calor absorvido da fonte quente?
Bom, temos achar em qual processo isso acontece. Temos 4 processos: 2 adiabáticos e 2 isotérmicos.
O calor não pode ter sido absorvido em nenhum dos dois adiabáticos, já que ali não há troca de calor, certo?
Então nos restam os processos isotérmicos. Em um dos processos isotérmicos, há um aumento de entropia, enquanto no outro há uma diminuição.
Entropia geralmente aumenta com o acréscimo de calor, não é mesmo? Já que a entropia mede a desordem de um sistema e acrescentar calor em um sistema não poderia deixar ele mais ordenado, só mais desordenado ( já que você tá enfiando mais energia nele).
Então o processo onde há ganho de calor é o processo . O calor dele a gente já calculou:
Então:
Passo 7
Vamos agora comparar a eficiência desse ciclo com a eficiência de um ciclo de Carnot operando entre as temperaturas extremas.
Bem, mas podemos resolver de outra forma.
Na nossa teoria, a gente viu que um ciclo de Carnot operando em um diagrama fica assim:
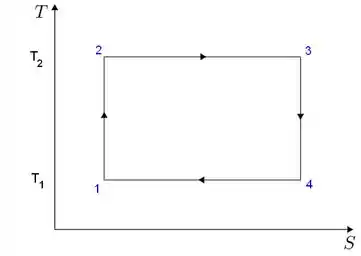
Beleza?
Bem, mas lembra que é função de Não só isso, é um função linear já que:
Então, isso quer dizer que um ciclo de Carnot operando num diagrama vai ter o mesmo formato que o formato acima.
Opa, mas é o formato que o enunciado nos dá:
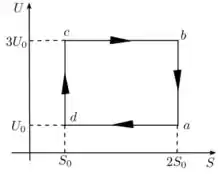
Conclusão: Esse é um ciclo de Carnot! Você poderia ter deduzido isso, também, vendo que um ciclo de Carnot sempre é formado por dois processos isotérmicos e dois processos adiabáticos.
Resposta: Mesma eficiência que um ciclo de Carnot.
Resposta
Isotérmico.
Adiabático.
Isotérmico.
Adiabático.
; ; ; ; ;
Máquina térmica.
Mesma eficiência de um ciclo de Carnot.
Exercício Resolvido #4
Seja o ciclo abaixo, realizado por n moles de um gás ideal, no plano . Considere conhecidas as temperaturas e e a diferença de entropia .
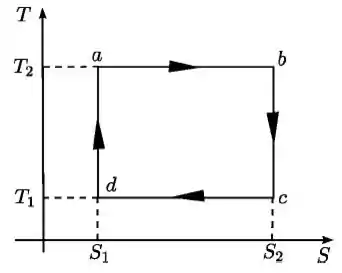
Calcule o trabalho total do ciclo em função de . Este ciclo representa uma máquina ou um refrigerador? Justifique.
Passo 1
Bom, olha só que malandragem vamos usar agora pra resolver essa questão de um jeito tranquilinho....Se liga na marotagem...
Para um ciclo, temos que a variação de energia interna é nula. Assim:
Então basta a gente calcular o calor total do ciclo! Olha só! Simples assim! ![]()
Já que:
Passo 2
Bom, como acabamos de calcular o trabalho para o ciclo e vimos que se trata de um valor positivo, chegamos à conclusão de que se trata de uma máquina térmica.
Resposta
Se trata, portanto, de uma Máquina Térmica
Exercício Resolvido #5
O ciclo de combustão interna de um motor a gasolina dos carros é conhecido como Ciclo Otto. O ciclo opera entre quatro processos, dois isocóricos (volume constante), onde ocorrem as trocas de calor, intercalados por dois adiabáticos, sem trocas de calor. No processo ocorre a queima do combustível na explosão fazendo com que a temperatura varie, e no processo ocorre o escape dos gases produtos da queima, variando a temperatura de . Suponha que os processo sejam quasi-estáticos e que o gás seja ideal.
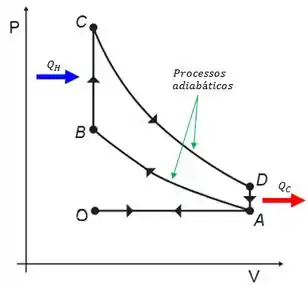
Represente o Ciclo Otto num diagrama .
Passo 1
Os processos são adiabáticos. Neles, não ocorre variação de entropia, assim, a entropia é constante. No diagrama, isso vai aparecer como retas verticais.
Já os outros dois processos são logarítimicos. Afinal de contas, aparecem logaritmos nas expressões das variações. Uma vez que o ponto é o que apresenta maior temperatura, conseguimos esboçar um diagrama com uma cara mais ou menos assim:
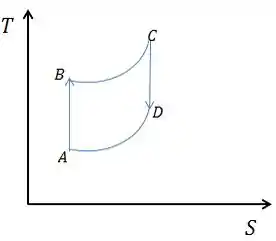
Resposta