Variação de Entropia: Gás ideal
Produzido por Leonardo de BemTeoria
Opaa! Bora aprender sobre a variação de entropia com o RespondeAí?!
A segunda lei da termodinâmica diz que que a variação de entropia do universo tende sempre a aumentar.
A entropia,
Como poderíamos calcular a variação de entropia do sistema abaixo?
A resposta é: Depende!
Para um caso geral usamos então a seguinte equação para a variação da entropia:
Onde
Mas para cada situação vamos usar uma formulazinha especial, como a gente pode ver nessa tabela resumo 👇
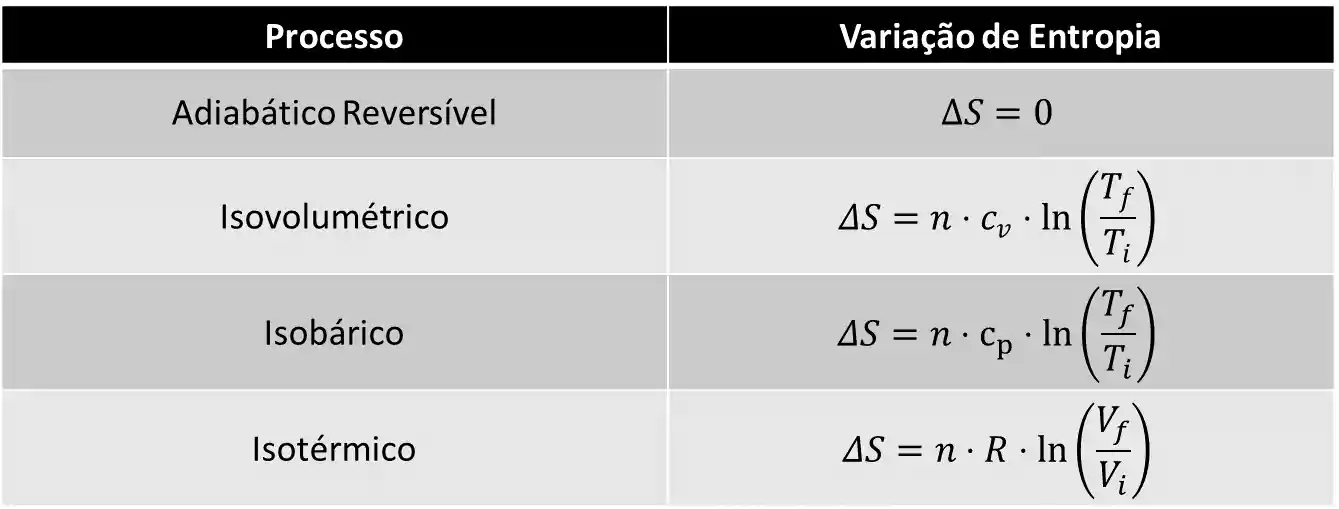
-Mas eu preciso decorar todas essas fórmulas?
Não, fica calmo! 🤣🤣🤣 Vamos entender da onde surge esse monte e fórmula e como chegamos nela a partir da fórmula geral!
Cálculo da Variação de Entropia
Vamos considerar 4 casos para os gases ideais. Processo adiabático reversível, isovolumétrico, isobárico e isotérmico.
Agora vamos ver como cada caso funciona!
Processo Adiabático Reversível
Nesse processo não há troca de calor no sistema portanto o calor absorvido pelas moléculas,
Então:
É um processo em que a entropia não varia, chamado de isentrópico!
Processo Isovolumétrico
No processo isovolumétrico não há variação do volume do gás, ele não se expande e nem se comprime.
Aqui precisaremos calcular o calor pra substituir na equação da entropia. Isso porquê no caso isovolumétrico o calor depende da variação de temperatura, então a integral deixará de ser em função do calor pra ser em função da temperatura.
Como calcular o calor nesse processo? Basta lembrar que:
E por isso temos:
Substituindo o
Como para um gás ideal
Integrando:
Então se te pedissem pra calcular um gás num processo isovolumétrico você precisaria somente das constantes:
que é o número de moléculas em mols do gás. que é o calor específico ao volume constante do gás que pro gás ideal é dada por: Onde
é a constante dos gases reais e é a constante pra cada tipo de gás (monoatômico, diatômico, poliatômico.) e são as temperaturas inicial e final do gás, respectivamente. Só fique atento as unidades, se o calor específico for dado em
a temperatura deverá ser em .
Processo Isobárico
Aqui não há variação de pressão e o calor será como no volumétrico uma função da temperatura.
A única diferença aqui é que usaremos o calor específico para pressão constante
Se jogarmos na equação da entropia e integrarmos, vai dar:
A única coisa nova aqui é o calor específico na pressão constante
Processo Isotérmico
Nesse processo a temperatura não varia e portanto a variação da energia interna do gás
Isso influencia diretamente a primeira lei da termodinâmica:
Lembrando que o trabalho aqui é dado por:
Substituindo na integral da entropia temos:
Só que agora a pressão não é constante com o volume. Temos que transformar as coisas, usando o a lei dos gases ideais:
Substituindo na integral
Resolvendo a integral:
Então pro processo isotérmico em relação ao que já vimos antes só vamos depender das constantes,
Se você quiser entender mais de transformações gasosas pode clicar aqui!
Agora que já entendemos como calcular a variação de entropia pra gases ideais, podemos ver uma aplicação muito utilizada!
A variação de entropia nos ciclos termodinâmicos! Clica aqui em baixo pra conferir 👇
Bora praticar com exercícios?!