Exercícios Resolvidos de Fontes de Tensão e de Corrente e Instrumentos de Medição
Ver TeoriaEnunciado
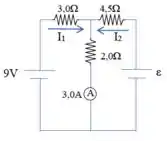
O amperímetro marca . Determine os valores de e .
Passo 1
Para resolver esse circuito, vamos usar a lei das malhas. Vamos considerar a primeira malha, a malha da esquerda e a segunda malha, a da direita.
Pela lei dos nós, já sabemos que , pois essa é a corrente no ramo em que as correntes se somam.
Na primeira malha, adotando o sentido da corrente temos:
Portanto, temos que:
Agora que já temos os valores das correntes, basta analisar a segunda malha para determinar .
Passo 2
Analisando a segunda malha, no sentido da corrente, temos:
Resposta
Exercícios de Livros Relacionados
a) A interconexão na Figura P2.8 é válida? Explique. b) Você pode determinar a energia total relacionada ao circuito? Explique.
A interconexão de fontes ideais pode resultar em uma solução indeterminada. Com isso em mente, explique por que as soluções para v1 e v2 no circuito da Figura P2.5 não são únicas.
Se a interconexão na Figura P2.9 é válida, determine a potência total fornecida ao circuito. Se a interconexão não é válida, explique a razão.
Considere a interligação mostrada na Figura P2.7. a) Qual é o valor de a necessário para tornar válida essa interligação? b) Para esse valor de a, determine a potência associada à fonte de corrente. c
a) Use transformações de fonte para determinar v 0 no circuito da Figura P4.63.b) Determine a potência gerada pela fonte de 520 V.c) Determine a potência gerada pela fonte de corrente de 1 A.d) Verifi