Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fontes de Tensão e de Corrente e Instrumentos de Medição

Ver Teoria
Exercício 71234568910

Enunciado

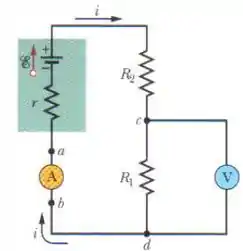
Na figura abaixo suponha que ε = 3 V ,   r = 100 Ω ,   R 1 = 250 Ω   e   R 2 = 300 Ω . Se a resistência do voltímetro R V é 5 k Ω ,   que erro percentual o voltímetro introduz na medida da diferença de potencial entre os terminais de R 1 ? Ignore a presença do amperímetro.

,

Passo 1

Aqui temos mais um circuito com mais de uma malha. Logo, de cara já sabemos que teremos que usar as Leis de Kirchhoff, tanto nos nós quanto nas malhas.

O erro percentual no potencial pode ser calculado pela divisão entre a ddp gasta pelo resistor R 1 se ele tivesse com ou sem voltímetro ligado em paralelo, e pra poder calcular isso temos que achar o valor da corrente nos dois casos. Vamos procurá-la

Passo 2

Aplicando a Lei de Kirchhoff na malha da esquerda utilizando a direção de corrente dada, teremos:

ε - r i - R 2 i - R 1 i 1 = 0

Já aplicando na malha da direita, teremos:

- R V . i 2 + R 1 i 1 = 0

Passo 3

Mas ah, pela Lei dos nós no nó C, teremos:

i = i 1 + i 2

i 2 = i - i 1

Substituindo na ultima equação do passo anterior, vai ficar:

R 1 i 1 - R v i - i 1 = 0

i = R 1 + R v R V i 1

Agora substituindo na primeira equação, vamos ter:

ε - r R 1 + R v R V i 1 - R 2 . R 1 + R v R V i 1 - R 1 i 1 = 0

ε - i 1 r + R 2 R 1 + R V + R 1 R V R V = 0

i 1 = ε R V r + R 2 R 1 + R V + R 1 R V

Passo 4

Achando o potencial entre os terminais do resistor R 1 , vamos ter:

V 1 = R 1 . i 1 = ε R V R 1 r + R 2 R 1 + R V + R 1 R V = 3.5000.250 100 + 300 250 + 5000 + 5000.250 = 1,12 V

Passo 5

Se não houvesse o voltímetro, teríamos uma malha única e a corrente seria apenas i , calculada, usando a Lei das Malhas, por:

ε = i [ r + R 1 + R 2 ]

i = ε r + R 1 + R 2

E o potencial seria calculado por:

V ' = ε R 1 r + R 1 + R 2 = 3.250 100 + 250 + 300 = 1,15 V

Logo, o erro percentual vai ser calculado pela diferença percentual entre esses dois valores, dado por:

e = 1,15 - 1,12 1,15 = 3 %

Resposta

e = 3 %

Exercícios de Livros Relacionados

a) A interconexão na Figura P2.8 é válida? Explique. b) Você pode determinar a energia total relacionada ao circuito? Explique.
A interconexão de fontes ideais pode resultar em uma solução indeterminada. Com isso em mente, explique por que as soluções para v1 e v2 no circuito da Figura P2.5 não são únicas.
Se a interconexão na Figura P2.9 é válida, determine a potência total fornecida ao circuito. Se a interconexão não é válida, explique a razão.
Considere a interligação mostrada na Figura P2.7. a) Qual é o valor de a necessário para tornar válida essa interligação? b) Para esse valor de a, determine a potência associada à fonte de corrente. c
a) Use transformações de fonte para determinar v 0 no circuito da Figura P4.63.b) Determine a potência gerada pela fonte de 520 V.c) Determine a potência gerada pela fonte de corrente de 1 A.d) Verifi