Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Funções definidas por partes

Ver Teoria
Exercício 3124

Enunciado

UFF, Cálculo IA-Lista 3, GMA, 2008-1, Questão 02.

Dadas as funções f x = x 2 + 3       s e   x ≤ 1 x + 1       s e   x > 1 e g x = x 2       s e   x ≤ 1 2       s e   x > 1 ,

i Esboce o gráfico de f e g .

Passo 1

Para facilitar na hora do esboço, vamos traçar cada uma das expressões ignorando os intervalos e depois limitamos o gráfico.

Vamos começar com f e a expressão x 2 + 3 . Veja que:

x 2 + 3 = 1 ⋅ x 2 + 3 ⟹ 1 > 0

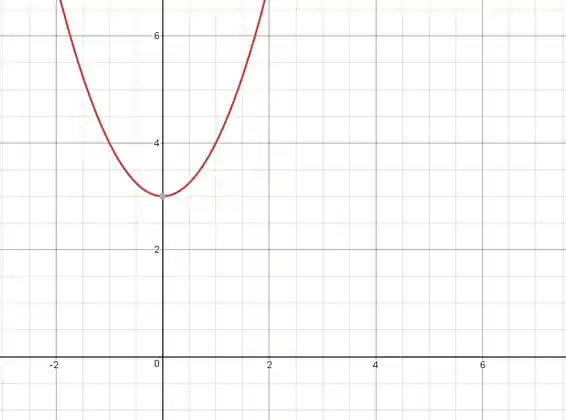
Com isso, é uma parábola côncava para cima. Também cruzará o eixo y , em x = 0 : 0 2 + 3 = 3 ⇒ y = 3 Resultando em:

Passo 2

Vamos agora para a segunda expressão de f : x + 1 , que é uma reta. Veja que:

x + 1 = 1 ⋅ x + 1 ⇒ 1 > 0

Logo a reta é crescente. Também cruzará o eixo y em x = 0 :

0 + 1 = 1 ⟹ y = 1

E o eixo x em y = 0 :

x + 1 = 0 ⟹ x = - 1

Resultando no gráfico: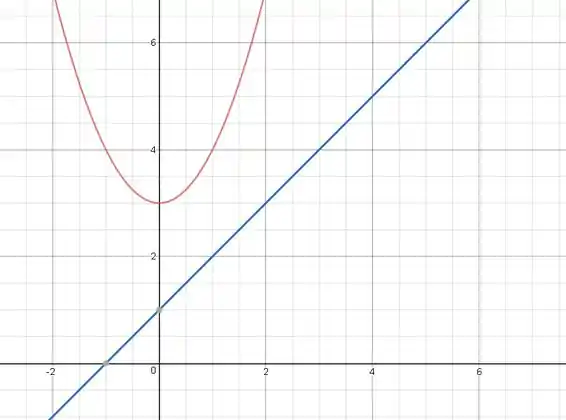

Passo 3

Vamos agora aplicar os intervalos. A primeira expressão é válida para valores de x ≤ 1 . Enquanto a segunda é válida para valores de x > 1 .

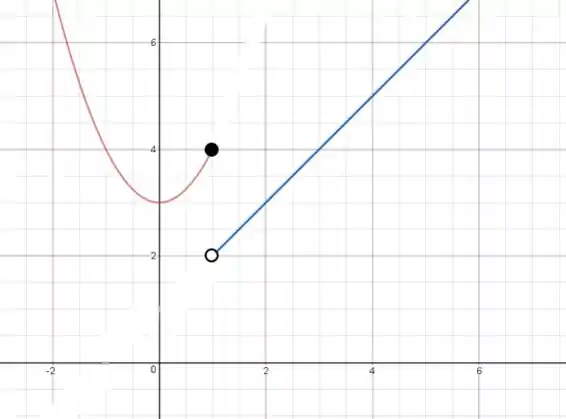
Como temos o sinal de menor ou igual no intervalo da primeira expressão, o ponto x = 1 tem essa expressão e recebe, portanto, uma bolinha de recheio preto, enquanto a expressão adjacente fica com bolinha de recheio branco:

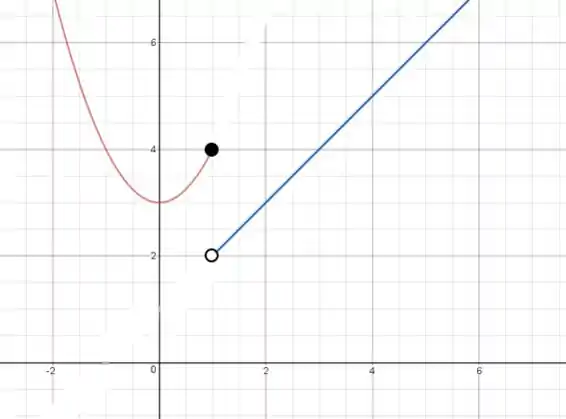
Pronto, esboçado!

Passo 4

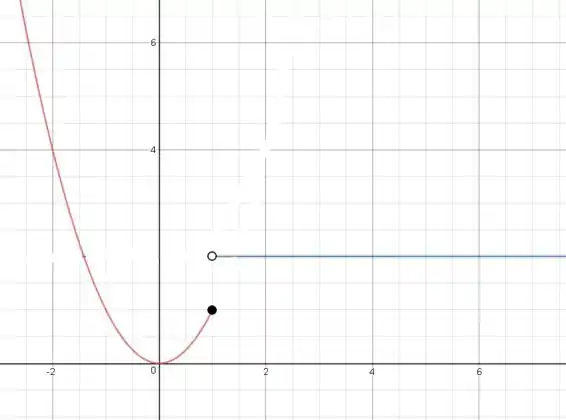
Vamos esboçar o gráfico de g seguindo o mesmo princípio. A primeira expressão é x 2 que é uma parábola côncava para cima na origem:

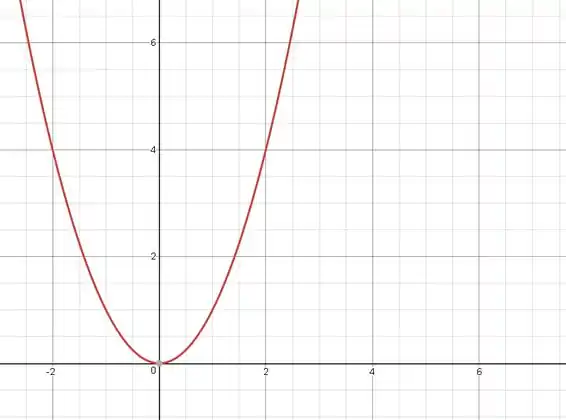
Enquanto a segunda expressão é a constante y = 2 :

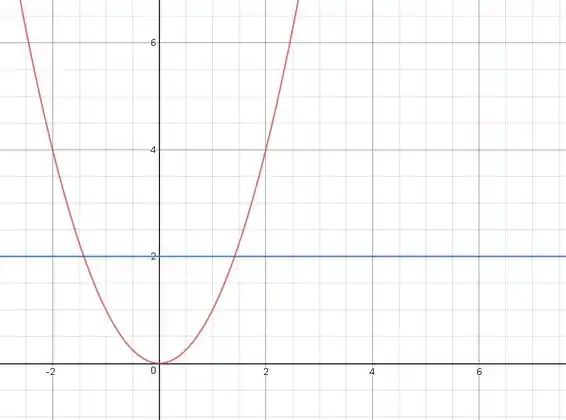
Temos também exatamente os mesmos intervalos de f resultando em:

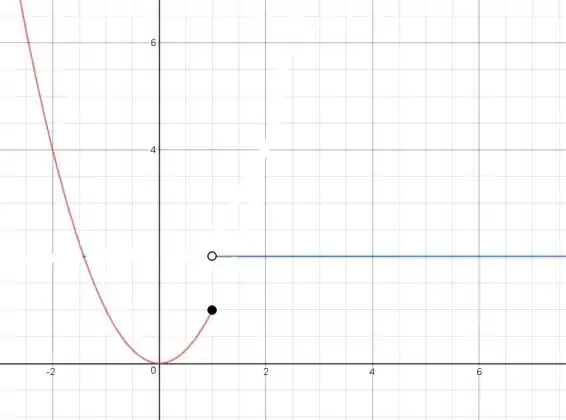
Resposta