UFF, Cálculo IA-Lista 1, GMA, 2008-1, 45
Esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
Passo 1
Temos que:
Dessa maneira, podemos abrir a função mais ainda:
Vamos esboçar cada parábola e depois segmentar os intervalos.
Passo 2
Para a primeira expressão:
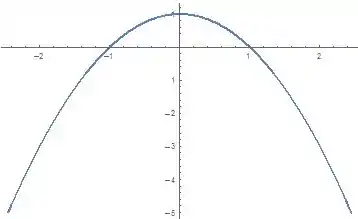
Segunda:
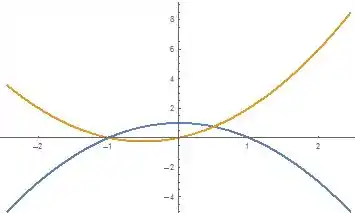
Finalmente:
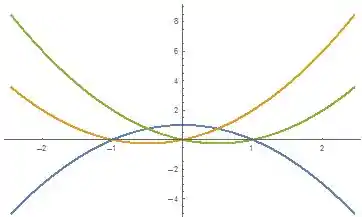
Passo 3
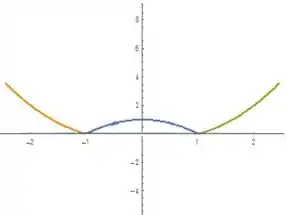
Sabendo que a primeira é válida para , a segunda para e a terceira para , chegamos em:
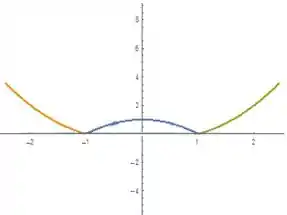
Como podemos perceber, a função é simétrica em relação ao eixo e é, portanto, par.
Passo 4
Quanto ao domínio, todas as funções são polinômios e, dessa maneira, o domínio será igual ao conjunto dos números reais:
Quanto a imagens, vemos que a função nunca é negativa, mas pode atingir qualquer valor maior que zero, dessa maneira:
Resposta
A função é par
.