Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Funções definidas por partes

Ver Teoria
Exercício 2134

Enunciado

Determine os valores máximos e mínimos da seguinte função:

f x = sen ⁡ x ,     x < π x 2 - π x ,     x ≥ π

Passo 1

Temos que a função tem expressão sen ⁡ x para todo x < π . Enquanto x 2 - π x tem raízes:

x 1 = 0 x 2 = π

E vértice:

x v = - b 2 a = π 2

E:

y v = - Δ 4 a = - π 2 4

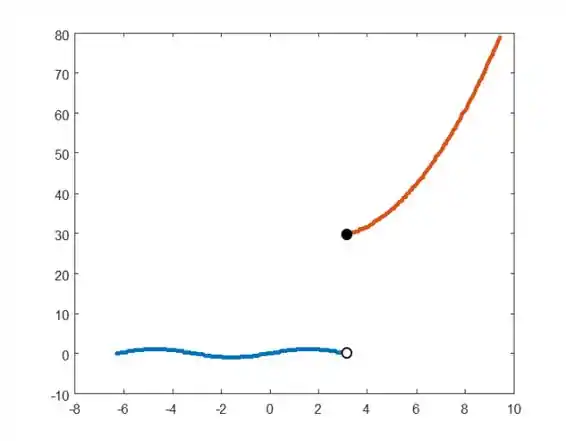
Formando o gráfico:

Passo 2

Observando a função, vemos que não tem ponto de máximo, pois a parte da parábola cresce indefinidamente e o mínimo é ditado pelos mínimos do seno que começam x = - π / 2 e se repetem a cada 2 π indo para a esquerda.

Resposta

Pontos de máximo: não há

Pontos de mínimo: - π 2 - 2 π ⋅ k ,   k = 0,1 , 2,3 …