Determine a estrutura dividida com o arranjo de incógnitas simétricos e assimétricos, e determine a relação necessária para o cálculo dos esforços reais.
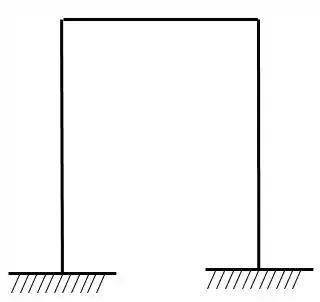
Passo 1
Fala, pessoal!!! Essa questão aqui é boa para trabalhar o conceito de grupo de incógnitas em estruturas simétricas porque é uma das formas mais simples que isso pode ficar.
Para resolver essa questão a gente só precisa quebrar os vínculos nos lugares corretos e achar os respectivos sistemas e equações. Então vamos lá?
Passo 2
Primeiro temos que definir o número de hiperestáticos da nossa estrutura.
- Sabemos que temos 2 apoios do terceiro gênero
- Ao todo então temos 6 incógnitas no nosso problema
- Como não tem nenhuma rótula, temos no total 3 equações de equilíbrio
- Logo fazendo a continha:
Logo precisamos quebrar 3 vínculos, simetricamente. Essa quebra vai ser o da seguinte maneira.
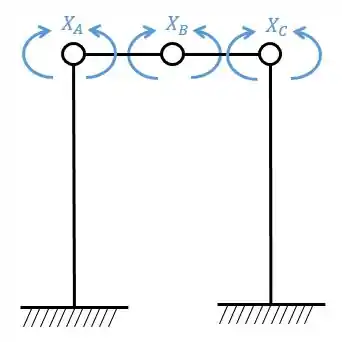
Passo 3
Agora precisamos dividir os sistemas simétricos e assimétricos, em que teremos a seguinte divisão.
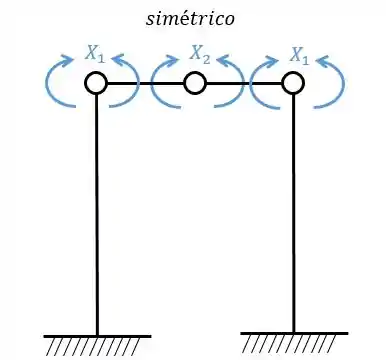
- Sistema simétrico
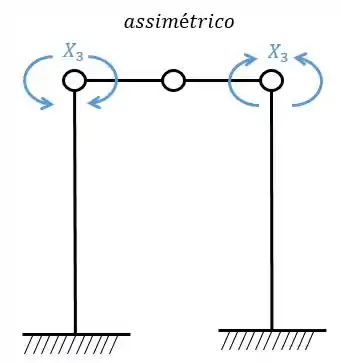
- Sistema assimétrico
- Sistemas de relação entre o grupo de incógnitas
- Sistema simétrico
- Sistema Assimétrico
- Sistema de equações
- Grupo de incógnitas
Passo 4
Por fim, precisamos apenas dividir os sistemas que precisamos desenhar os diagramas.
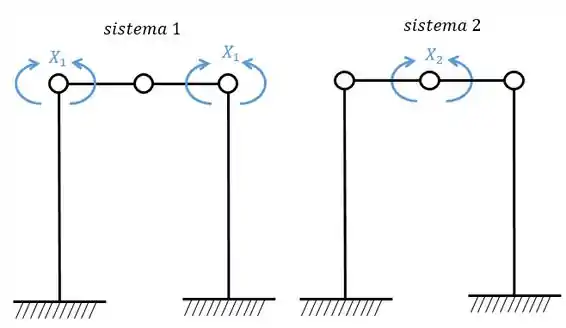
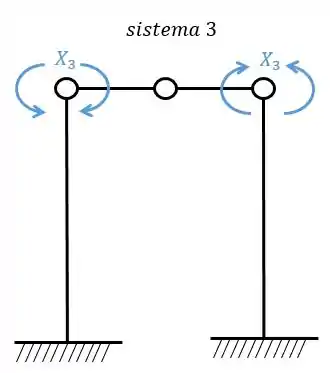
Agora a gente tem que perceber algumas coisas: os sistemas simétricos (1 e 2) irão gerar as deformações relativas entre si.
Enquanto os sistemas assimétricos (3) também geram deformações relativas entre si, no caso apenas.
Passo 5
Agora antes de montar a matriz a gente tem que lembrar que a combinação de sistemas simétricos com assimétricos é sempre nula! Logo, vamos ter para os sistemas simétricos:
Para os sistema assimétricos:
Repare que poderíamos colocar como uma matriz se quiséssemos =D
Resposta
Sistemas criados e sua simetria ou assimetria
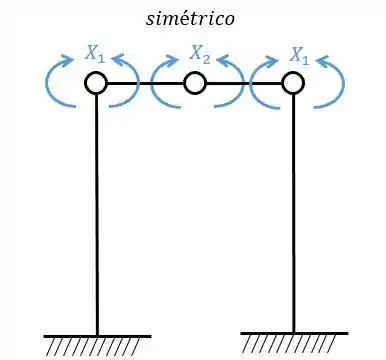
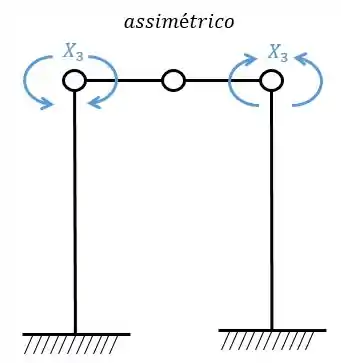
Resposta
Ei, a resposta está no passo a passo :)