2°EE de Cálculo Numérico da UFPE - 2019.2
Cálculo Numérico - UFPE
3. Complete o programa abaixo para implementar o método de resolução de sistemas lineares de Gauss-Seidel. Considere que as funções carregarSistemaLinear, diferencaMaxima e imprimirX já estejam implementadas.

1. Dado o sistema linear:
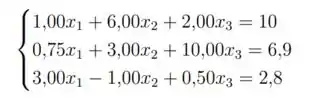
- Reescreva o sistema linear de forma a garantir sua convergência pelo método de Jacobi (diagonal estritamente dominante por linha).
- Escreva as expressões das sequências obtidas pelos métodos de Jacobi e Gauss-Seidel (i.e., o motor gerador de cada incógnita) para o problema acima.
- Calcule duas iterações do método de Gauss-Seidel com vetor inicial x(0) = (0; 0; 0)T .
2. Considerando os pontos da tabela abaixo:
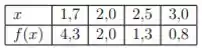
a) Ajuste a função aos pontos dados. Obs.: O sistema linear resultante deve ser resolvido pelo método de eliminação de Gauss.
b) Calcule o valor de a partir do modelo encontrado.
c) Baseado no erro quadrado, indique se o modelo encontrado em (a) é mais preciso do que a opção linear .
Ver solução completa