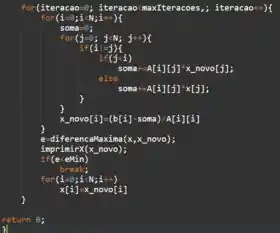
3. Complete o programa abaixo para implementar o método de resolução de sistemas lineares de Gauss-Seidel. Considere que as funções carregarSistemaLinear, diferencaMaxima e imprimirX já estejam implementadas.

Passo 1
Falaaa, galera! Lembram do método de Gauss-Seidel? É mais um daqueles métodos para obter a solução de sistemas lineares! Nesse exercício vamos implementar o método de Gauss-Seidel por meio de um programa, o que vai nos ajudar muuuito, já que são várias continhas envolvidas no processo.
Para que o programa fique mais claro, vamos considerar um sistema com 2 equações e 2 incógnitas (e ), com a forma matricial .
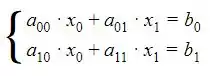
Para cada iteração, devemos efetuar os seguintes cálculos:
e
Sendo que o resultado nos fornece o novo vetor solução :) Mas não se esqueçam, galera, o cálculo do novo vetor solução sempre depende do vetor da iteração anterior! Exceto para primeira iteração, claro, que usamos o vetor inicial [0,0]!
Mas vocês devem estar se perguntando: qual é o critério de parada nesse caso??? Nós vamos parar após 50 iterações ou ao atingir o erro mínimo de 0.0001. Mas não se preocupem com este erro, pois o enunciado já nos forneceu uma função para calculá-lo (diferencaMaxima).
Passo 2
Beleza, pessoal, agora que relembramos o método, vamos entender a parte do programa já implementada!
O primeiro passo é declarar as funções fornecidas pelo enunciado (carregarSistemaLinear, diferencaMaxima e imprimirX). Devemos fazer isso antes de começar o programa para não termos nenhum tipo de erro, beleza? Já voltamos nelas!
Em seguida, vamos declarar todas as variáveis usadas durante o programa. Como já comentamos, as variáveis A, b e x representam nosso sistema na forma matricial! A variável x_novo conterá a nova solução para o sistema calculada em cada iteração. Todos dependem da dimensão N, que como já comentamos, será 2 para o nosso exemplo, já que temos um sistema 2x2.
As variáveis i, j, iteracao, e e soma são auxiliares, vamos entender logo mais a importância delas! As variáveis maxIteracoes e eMin são os nossos critérios de parada, ou seja, 50 e 0.0001, nessa ordem.
Uma vez que já temos nossas variáveis declaradas, vamos usar a função carregarSistemaLinear para definir os valores da matriz A e do vetor b (ou seja, os valores de e ). Em seguida, vamos zerar o vetor x, utilizando uma laço de repetição for, para que a solução inicial seja e ! E, antes de finalmente começar as iterações, vamos atribuir valores aos critérios de parada, como já comentamos, né?
Passo 3
Ufa, finalmente vamos a parte mais importante, as iterações! Vamos ter um código assim:
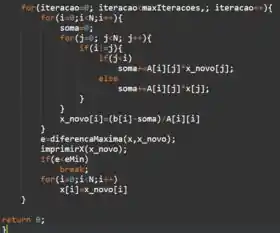
Vamos começar com um laço de repetição for que vai rodar da iteração 0 até a iteração máxima (maxIteracoes=50), uma por uma. Vamos usar mais dois laços de repetição for para rodar a matriz A, sendo um para as linhas e outro para as colunas. Veja que nesta parte já usamos três variáveis auxiliares: iteracao, i e j.
Beleza, pessoal, essa é a parte mais complicada, então vamos com calma! Eu acabei de falar que os dois laços servem para rodar a matriz A, certo? Isso significa passar por e , um por um. Vamos fazer isso então, usando a notação do programa:
a[0][0]:
i = 0
soma = 0
j = 0
Como i é igual a j, não entramos no primeiro condicional if.
a[0][1]:
i = 0
j = 1
Como i é diferente de j, entramos no primeiro condicional if.
Como j é maior que i, entramos no condicional else.
soma = A[0][1]*x[1]
x_novo[0] = (b[0] - soma)/A[0][0]
a[1][0]:
i = 1
soma = 0
j = 0
Como i é diferente de j, entramos no primeiro condicional if.
Como j é menor que i, entramos no segundo condicional if.
soma = A[1][0]*x_novo[0]
a[1][1]:
i = 1
j = 1
Como i é igual a j, não entramos no primeiro condicional if.
x_novo[1] = (b[1] - soma)/A[1][1]
Veja então que x_novo[0] = (b[0] - A[0][1]*x[1])/A[0][0] e x_novo[1] = (b[1] - A[1][0]*x[0])/A[1][1]. Ou em uma linguagem mais clara:
e
Exatamente como vimos no passo 1!
Veja então que o primeiro condicional controla quais termos devem ser somados na variável auxiliar soma. Mas como assim? Bem, se tivéssemos mais de 2 dimensões, teríamos o seguinte padrão:
Ou seja, o desafio de cada iteração é definir a “soma dos demais termos”, que ocorre linha por linha. Por isso que a cada mudança de linha, zeramos a variável soma.
O segundo condicional controla quais termos devem ser somados usando a solução nova (iteração atual), isto é, aqueles onde j
Ao final da iteração, vamos usar a função diferencaMaxima para calcular o erro entre a solução antiga (x) e a solução atual (x_novo), e atribuir à variável auxiliar e. Também usaremos a função imprimirX para imprimir a solução atual. O condicional if serve para verificar se o erro é menor que o erro mínimo (eMin); se este for o caso, o laço for das iterações será interrompido pelo comando break. Caso contrário, a nossa nova solução antiga será a solução atual (x=x_novo) e iremos para uma nova iteração, para calcular mais uma vez x_novo.
Resposta