2. Considerando os pontos da tabela abaixo:
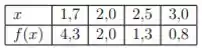
a) Ajuste a função aos pontos dados. Obs.: O sistema linear resultante deve ser resolvido pelo método de eliminação de Gauss.
b) Calcule o valor de a partir do modelo encontrado.
c) Baseado no erro quadrado, indique se o modelo encontrado em (a) é mais preciso do que a opção linear .
Passo 1
Eai, galera?? Vamos para mais um exercício de cálculo numérico! Bem, nós queremos ajustar a função aos 4 pontos da tabela, ou seja, descobrir os valores de e . Para isso, vamos usar o Método dos Mínimos Quadrados!
Observem primeiro que é uma função exponencial. Logo, devemos fazer uma linearização através de uma mudança de variável. Vamos considerar :
Agora nós temos um modelo linearizado , em que , , e . Em seguida, vamos obter os valores de , e para os pontos da tabela:
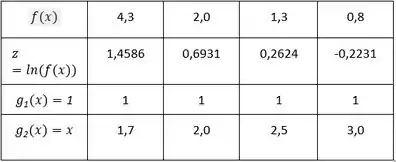
Para encontrar os coeficientes e da função , devemos resolver o seguinte sistema de equações:
Galera, a notação indica que devemos fazer o produto escalar entre os vetores e ! No caso das nossas equações, vamos considerar que e são vetores cujos elementos estão exibidos na tabela acima! Por exemplo:
De boa, né? Realizando esses seis produtos escalares, nós chegamos no seguinte:
Falta pouco, galera! Respira fundo hahaha Vamos usar o método de eliminação de Gauss para resolver esse sistema! Multiplicando a primeira linha por e somando com a segunda, obtemos:
Isolando em , achamos . Substituindo este valor em e isolando , achamos ! Como , então . Como , então . Ufa!
Passo 2
A letra B é moleza, hein? Nós vimos no passo 1 que . Para , teremos então:
Simples assim, apenas substituir o valor de na função !
Passo 3
Finalmente chegamos na última questão! Galera, para achar o erro quadrado, devemos calcular e para os valores de tabelados no enunciado, tranquilo? Resumindo tudo em uma tabela, vamos ter algo assim:
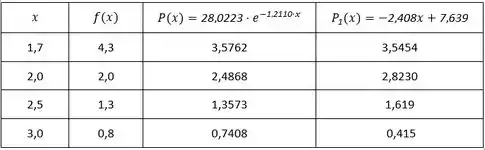
A fórmula do erro quadrático é: . Para e , teremos:
Vemos então que o erro quadrático de é o menor que o de . Valeu, galera!
Resposta
a) .
b) .
c) O modelo encontrado em (a) possui erro quadrático inferior ao da opção linear, sendo, portanto, mais preciso.