AV2 de Física 1 da UFJF - 2015.2

4 – Responda cada um dos itens:

a) Numa colisão totalmente inelástica entre dois corpos de massa e , onde está em repouso, qual deve ser a relação entre as massas e para que a velocidade final seja da velocidade inicial?

b) Considere uma colisão entre dois corpos ( e ) de massas iguais. O corpo está inicialmente em repouso. Após a colisão, a velocidade de cada um deles será necessariamente menor que a velocidade inicial do corpo . Ou seja, as constantes definidas como e são necessariamente menores que . Nestas definições os índices e (inicial e final) se referem às situações antes e depois da colisão respectivamente. Qual deve ser a relação entre as constantes e para que a colisão seja totalmente elástica?

2 – Duas partículas partem da origem, a primeira de massa com velocidade caracterizada por e a segunda, de massa e com velocidade .

As velocidades são relativas ao mesmo observador na origem. Determine:

a) Como o vetor centro de massa do sistema varia com o tempo?

b) em que ponto do espaço estará o centro de massa em ?

c) Neste instante, , qual é o vetor velocidade instantânea do centro de massa do sistema?

d) Qual o vetor força externa que atua sobre este sistema de partículas?

Dois blocos de massas e estão conectados por um cabo de massa muito pequena que passa por uma polia de massa também irrisória, que gira sem atrito, conforme mostra a figura ao lado. Considerando-se que na posição inicial a mola, de constante elástica , não exerce força sobre o bloco , calcule:

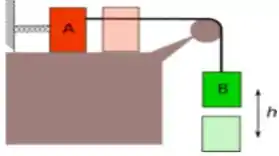
a) A máxima elongação (h) da mola quando o bloco desliza sem atrito.

b) A máxima elongação (h) da mola na presença de atrito, com coeficiente de atrito cinético .

Uma partícula está submetida ao potencial mostrado.

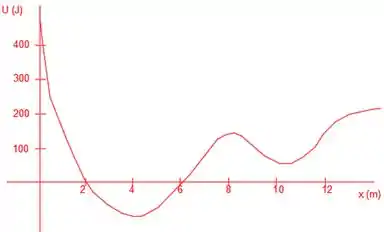
a) Faça o gráfico da força associada a esse potencial no intervalo de a.

b) Quais são os pontos de equilíbrios estável e instável? Justifique.

c) Se a partícula possui energia mecânica total igual a zero, em que intervalo no espaço ela pode ser encontrada? E se a sua energia total for ? Justifique.

d) Se sua energia total for de , qual sua velocidade no ponto ? Justifique.