AV2 de Física 1 da UFJF - 2016.1

1) Um corpo de massa está preso à extremidade de um fio ideal que está enrolado numa peça composta por dois cilindros de massas e e raios e , que giram juntos sobre um eixo, como mostra a figura. O fio está enrolado em torno do cilindro e não desliza sobre ele.

O momento de inercia de um cilindro maciço é dado por:

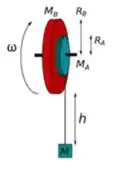
a) Faça um diagrama de corpo livre para o corpo de massa e para a peça composta por dois cilindros.

b) Suponha que não há perdas por atito. Use a 2ª Lei de Newton e seu análogo rotacional para calcular a aceleração do bloco de massa em função das variáveis dadas no problema.

Uma esfera sólida sobe rolando um plano inclinado, cujo ângulo de inclinação é igual a em relação a horizontal. Na base do plano, o centro de massa da esfera tem uma velocidade linear de . Seu momento de inércia em relação ao seu centro de massa é .

1. Qual é a energia cinética da esfera na base do plano inclinado?
2. Qual é a distância que a esfera percorre ao subir o plano?
3. A resposta do item b depende da massa da esfera? Comente.

Considere que um míssil de massa e velocidade inicial é lançado do solo fazendo um ângulo de como mesmo. Suponha que o míssil, ao alcançar sua altura máxima, se divide em duas partes: uma de massa e outra de massa , sendo que a parte com a massa menor cai verticalmente para baixo. Desprezando-se a resistência do ar e supondo que as duas partes tocam o solo ao mesmo tempo, calcule:

1. a posição em que o centro de massa das duas massas toca o solo.
2. a posição em que a parte com a massa maior toca o solo.

4 – Um projétil de massa é lançado com um ângulo com a horizontal, como mostra a figura, com velocidade inicial .

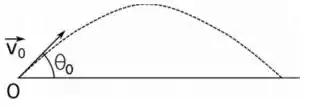
a) calcule o módulo do torque realizado pela gravidade sobre a bola de canhão, em relação ao ponto de lançamento , em .

b) Qual a direção e sentido do torque nesse instante?

c) Calcule o momento angular da bala de canhão em relação ao ponto , nesse mesmo instante.

d) Qual a direção e sentido do momento angular nesse instante?