UFJF – Fisica 1 – Provas - Teste 9 – AV2 – 2015.2 – Questão 1
Uma partícula está submetida ao potencial mostrado.
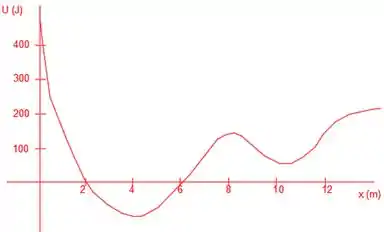
a) Faça o gráfico da força associada a esse potencial no intervalo de a.
b) Quais são os pontos de equilíbrios estável e instável? Justifique.
c) Se a partícula possui energia mecânica total igual a zero, em que intervalo no espaço ela pode ser encontrada? E se a sua energia total for ? Justifique.
d) Se sua energia total for de , qual sua velocidade no ponto ? Justifique.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um gráfico que mostra o comportamento da energia potencial de uma partícula em relação ao tempo.
A questão nos pede para fazer um gráfico que está relacionada ao comportamento dessa partícula e nos faz alguns questionamentos.
Não se preocupa lendo tudo isso de uma vez não, viu? Bora junto responder cada letrinha 😉
Passo 2
Bom... vamos começar pela letra a):
Do gráfico da Energia Potencial versus a posição , sabemos que a força é dada por:
Sabendo disso, temos:
- Se é crescente, é negativo;
- Se é decrescente, é positivo;
- Quando é uma reta horizontal , então em pontos de máximo ou mínimo.
A partir disso, podemos plotar o gráfico da seguinte forma:
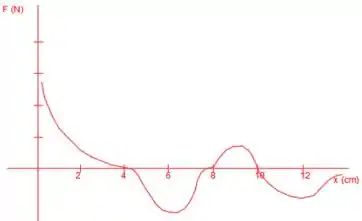
Passo 3
Para a letra b):
Sabemos que, por definição os pontos de equilíbrio estável ocorrem quando a função se encontra em seus mínimos locais.
Por outro lado, os pontos de equilíbrio instável ocorrem nos máximos locais.
Sendo assim, temos:
- Equilíbrio estável: e
- Equilíbrio instável:
Passo 4
Agora, na letra c):
Se a energia total do sistema é zero, a soma da energia potencial com a energia cinética da partícula deve se anular a todo momento.
No entanto, sabendo que a energia cinética pode ser apenas positiva, para que se anulem, a energia potencial deve ser exclusivamente negativa.
Logo, a partícula só pode estar em .
De forma análoga, caso a energia mecânica total seja , a partícula não poderá estar em pontos do gráfico onde a energia potencial é maior que esse valor...até porque isso exigiria uma energia cinética negativa.
Dessa forma, a partícula só pode estar em e (aproximadamente).
Passo 5
Agora, na letra d):
Como em , , temos:
Onde é a energia cinética, é energia potencial e é a energia total mecânica.
Em suma, toda a energia mecânica nesse sistema é dada como potencial!!
Entendeu direitinho? Responde aee ;)
Resposta
Na resolução