UFJF – Fisica 1 – Provas - Teste 9 – AV2 – 2015.2 – Questão 3
Dois blocos de massas e estão conectados por um cabo de massa muito pequena que passa por uma polia de massa também irrisória, que gira sem atrito, conforme mostra a figura ao lado. Considerando-se que na posição inicial a mola, de constante elástica , não exerce força sobre o bloco , calcule:
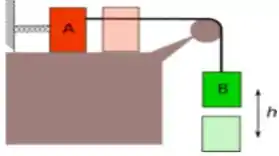
a) A máxima elongação (h) da mola quando o bloco desliza sem atrito.
b) A máxima elongação (h) da mola na presença de atrito, com coeficiente de atrito cinético .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um sistema com dois blocos conectados através de um cabo e nos pede para dizer o valor da elongação com e sem atrito quando o bloco desliza.
E aí? Alguma ideia para fazer isso?
Uma boa é usar as Leis de Newton!!
Ainda ficou na dúvida? Então bora junto!!
Passo 2
Bom... vamos começar pela letra a):
Quando o sistema entra em equilíbrio a força elástica da mola se iguala a força peso do bloco , que é a única força que atua para movimentar o sistema.
Sendo assim, temos que em uma situação de equilíbrio:
Ou seja:
Onde é a constante elástica da mola, é a deformação, é a massa do bloco e é a aceleração da gravidade.
Passo 3
Agora, na letra b):
Caso haja a presença de uma força de atrito entre o bloco e a superfície, ela atuará de forma contrária a força exercida pelo bloco .
Sendo assim, temos para as forças atuantes do sistema:
Entendeu direitinho? Responde aee ;)
