1) Um corpo de massa está preso à extremidade de um fio ideal que está enrolado numa peça composta por dois cilindros de massas e e raios e , que giram juntos sobre um eixo, como mostra a figura. O fio está enrolado em torno do cilindro e não desliza sobre ele.
O momento de inercia de um cilindro maciço é dado por:
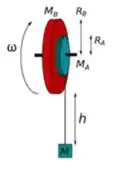
a) Faça um diagrama de corpo livre para o corpo de massa e para a peça composta por dois cilindros.
b) Suponha que não há perdas por atito. Use a 2ª Lei de Newton e seu análogo rotacional para calcular a aceleração do bloco de massa em função das variáveis dadas no problema.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão temos um eixo que nele está preso dois cilindros de massas e raios , , e . Ao redor do cilindro está enrolado um fio que na ponta tem um bloco de massa pendurado. Tudo isso podemos ver na imagem do enunciado.
O sistema gira no sentido que vemos na figura sendo que e .
Com isso queremos desenhar o diagrama de corpo livre para o bloco e para os dois cilindros no item a).
E no item b) temos que usar a 2ª Lei de Newton para obter a aceleração do bloco.
Como podemos fazer essas coisas? 🤔🤔
O diagrama de corpo livre pode ser feito imaginando quais forças agem em um objeto e como elas agem.
Com o diagrama, vamos analisar quais forças contribuem para a aceleração do bloco.
Sacou? Bora! 😁
Passo 2
Primeiro vamos fazer o diagrama para o bloco .
Podemos imaginar que há a ação da força peso devido a gravidade e a tração da corda
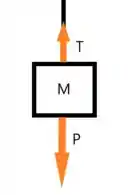
Agora para o bloco podemos imaginar que temo a força de rotação torque, a tração da corda que segura o bloco , a força peno e a força normal com o eixo de rotação.
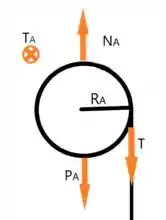
Já para o bloco imaginamos que temos as mesmas forças, com exceção da tração já que a corda não está enrolada nele
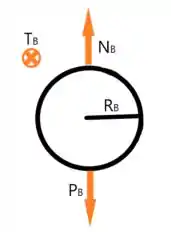
E aí, o que acha desses diagramas de corpo livre? Concorda? 🤔
Passo 3
Agora para obter a aceleração do bloco , temos que relacionar algumas forças.
O que queremos obter é a aceleração , não é?
Podemos relacionar com a aceleração angular de um movimento circular que é dado por
Onde é o raio de rotação, ou seja, o raio .
Já o torque de um movimento pode ser relacionado com a aceleração angular pela seguinte fórmula
Onde é o momento de inercia da rotação.
No enunciado foi dito que o momento de inercia de um cilindro é dado por
E como temos dois cilindros, podemos dizer que o momento total é dado por
Como e dizemos que
Substituindo e em , temos
Mas veja só, o torque também é a diferença entre a força peso e a tração na corda, não é? Se a tração fosse igual a força peso, o sistema estaria estático... concorda?
A força peso é dada por e a tração por
Igualando essas duas equações, temos
Vamos desenvolver melhor essa equação aqui...
Está entendendo? 😁
Passo 4
Podemos cortar dos dois lados para simplificar a equação.
Isolando , temos
Deixando o denominador igual nos termos de multiplicando por em cima e em baixo em , por em e por em , vamos obter
Passando o termo entre parênteses para o outro lado dividindo...
E é essa a aceleração que encontramos para o bloco na situação do enunciado!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta
a) Imagens no Passo 2.
b)