4 – Um projétil de massa é lançado com um ângulo com a horizontal, como mostra a figura, com velocidade inicial .
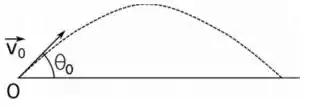
a) calcule o módulo do torque realizado pela gravidade sobre a bola de canhão, em relação ao ponto de lançamento , em .
b) Qual a direção e sentido do torque nesse instante?
c) Calcule o momento angular da bala de canhão em relação ao ponto , nesse mesmo instante.
d) Qual a direção e sentido do momento angular nesse instante?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Temos a seguinte situação nesse problema: temos um canhão carregado que está inclinado a da horizontal. O projétil que é lançado tem massa e o modulo da velocidade inicial é .
Diante disso, temos que descobrir qual é o modulo do torque que a força gravitacional faz com o projétil em relação ao canhão no instante . Também queremos saber qual é a direção e sentido desse torque.
Além disso, queremos calcular o módulo do momento linear do projétil nesse mesmo instante e sua direção e sentido.
Bastante coisa, não é? Como podemos fazer isso? 🤔
Observamos que esse é um movimento balístico e nesse tipo de movimento, o objeto faz um movimento uniforme na componente do eixo e um movimento acelerado na componente do eixo .
Com isso, vamos encontrar a velocidade inicial em e para descobrir como o projétil se comporta em
E assim calculamos seu o torque e o momento angular!
Preparado? Bora! 😉
Passo 2
Por analise vetorial, vamos obter a velocidade inicial em cada componente.
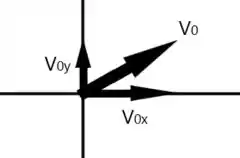
O ângulo que o vetor faz com a horizontal é então se o cosseno de um ângulo é dado pela razão entre o cateto adjacente sobre a hipotenusa e o seno pela razão entre o cateto oposto sobre a hipotenusa, temos que
Se foi dado como , então
Como em a velocidade é constante, durante todo o trajeto a velocidade
Já a velocidade em no instante , vamos usar a fórmula do voat, conhece?
No caso, a aceleração é a aceleração gravitacional que aponta para baixo, portanto,
Assim vemos que no instante o projétil está em seu ponto máximo e sua velocidade em é nula.
Entendeu essa parte? 👀
Passo 3
Agora temos que descobrir qual é a distância do projétil até o ponto de partida. Pra isso vamos usar a fórmula do sorvete e do sorvetão, conhece?
Primeiro com ralação a temos que é o valor que estamos procurando. é o valor inicial, ou seja, . é e
Agora com relação a temos que é o valor que vamos encontrar, é o valor inicial em , calculamos como , é a aceleração gravitacional e .
Então no ponto mais alto a distância do ponto de partida é dada por
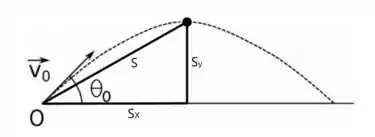
Agora vamos montar o vetor que é dado pelas componentes de cada eixo
E essa é a distância do projétil até o ponto !
Bacana, não é? 😎
Passo 4
E finalmente vamos obter o torque que a força gravitacional faz no projétil em relação ao ponto .
O torque é calculado como
Mas que força é essa?
Se a força é a massa multiplicada pela aceleração, então
Substituindo em
Calculando esse produto vetorial pelo método do determinante, temos
Então, para o item a) podemos obter que o valor absoluto do torque é dado por
Já no item b) temos que dizer qual é a direção e o sentido do torque.
Como obtemos no vetor torque que calculamos, o torque aponta para o sentido negativo do eixo .
Está acompanhando? 👀
Passo 5
Agora nosso objetivo está obter o momento angular do projétil no instante !
O momento angular é dado pela fórmula
já temos, já temos e podemos obter dado que temos as componentes da velocidade nesse instante
Como e nesse momento, então
Substituindo , e em , temos
Pelo método do determinante...
Fazendo a mesma análise que fizemos anteriormente para responder a letra c), temos que o valor absoluto de é dado por
E analisando o vetor, vemos que aponta para o mesmo sentido e direção do torque, sentido negativo do eixo .
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
a)
b) Sentido negativo do eixo
c)
d) Sentido negativo do eixo