UFJF – Fisica 1 – Provas - Teste 9 – AV2 – 2016.1 – Questão 3
Considere que um míssil de massa e velocidade inicial é lançado do solo fazendo um ângulo de como mesmo. Suponha que o míssil, ao alcançar sua altura máxima, se divide em duas partes: uma de massa e outra de massa , sendo que a parte com a massa menor cai verticalmente para baixo. Desprezando-se a resistência do ar e supondo que as duas partes tocam o solo ao mesmo tempo, calcule:
- a posição em que o centro de massa das duas massas toca o solo.
- a posição em que a parte com a massa maior toca o solo.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos fala sobre um lançamento oblíquo (que é composto por dois movimentos independentes, um horizontal e um vertical) de um míssil.
Quando o míssil atinge a altura máxima, ele se divide em duas partes com massas distintas, em que uma cai verticalmente.
Assim, para podemos enxergar melhor o que a questão está nos dizendo, veja a figura abaixo:
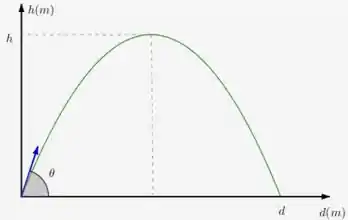
Onde é a altura e é a distância.
Queremos descobrir a distância em que o centro de massa das duas massas toca o solo e a distância em que a parte com a massa maior toca o solo.
Ainda ficou na dúvida? Então bora junto!!
Passo 2
Bom... vamos começar pela letra a):
Antes do míssil se dividir, o centro de massa percorre uma trajetória fixa de um lançamento oblíquo convencional.
Após a separação no topo da trajetória, como não foram aplicadas forças externas ao sistema, o centro de massa continuará seguindo a mesma trajetória.
Dessa forma, o ponto em que o centro de massa do sistema toca o solo é o alcance do míssil de massa caso ele não se dividisse.
Passo 3
Sendo assim, temos que o tempo de subida é dado por:
Onde é a velocidade inicial e é a aceleração da gravidade.
E o seu alcance é dado por:
Passo 4
Agora, na letra b):
Considerando o eixo horizontal que contém as perdas do míssil e seu centro de massa, determinamos a distância da parte de maior massa pela média ponderada a seguir (observe a figura):
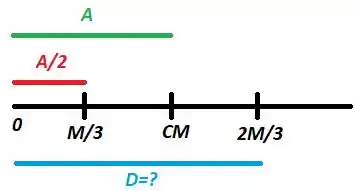
Entendeu direitinho? Responde aee ;)
