P3 de Física 1 da UNICAMP - 2012.1 Manhã

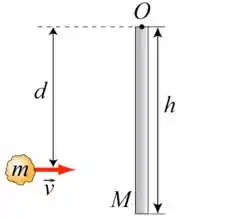
Uma barra homogênea de massa e comprimento pode girar em torno de um eixo fixo (ponto O) em uma de suas extremidades. Uma bola de massa de modelar, com massa e velocidade , atinge a barra a uma distância do eixo e fica grudada na barra. Dado: O momento de inércia e uma haste de massa e comprimento h em relação a um eixo que passa pelo seu centro de massa é

Momento de inércia de uma barra: .

1. Que grandezas são conservadas durante a colisão? Justifique sua resposta.
2. Qual o momento de inércia do sistema bola+barra em relação ao ponto O ?
3. Qual o momento angular do sistema após a colisão em relação ao ponto O ?
4. Qual a razão entre a energia final e a energia inicial do sistema?

Um brinquedo comum de criança consiste em duas pequenas esferas de madeira amarradas por um fio, de massa desprezível e comprimento , e que são postas para colidir acima e abaixo do ponto de sustentação. No instante retratado pelo desenho, cada bola tem uma velocidade linear e o fio está esticado. Considere que o eixo de rotação é fixo.

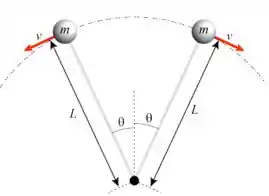
1. Desenhe as forças atuando em cada esfera no instante mostrado no desenho.
2. Calcule o módulo das acelerações centrípeta e tangencial em cada esfera.
3. Qual é a tração no fio neste instante ?
4. Calcule os torques da força peso e tração em cada uma das esferas, indicando direção e sentido, em relação ao eixo de rotação fixo.
5. Calcule o momento angular de cada bola em relação ao eixo de rotação fixo, e o momento angular total do sistema.

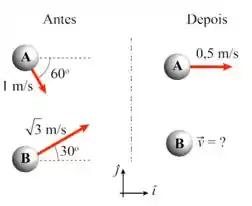
Duas partículas colidem numa superfície sem atrito. As velocidades de ambas antes da colisão são mostradas na figura ao lado. Após a colisão, a partícula A move-se com . Considere que a massa da partícula é o dobro da massa da partícula , ou seja, .

1. Qual é a velocidade do centro de massa do sistema antes da colisão?
2. Encontre o vetor velocidade da partícula B após a colisão.
3. A colisão é elástica? Justifique sua resposta

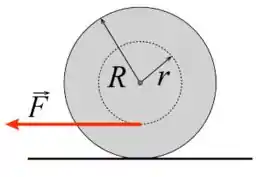
Um carretel de massa e raio externo rola sem deslizar, para a esquerda, ao ser puxado por uma força aplicada ao seu raio interno como mostra a figura. Sabe-se que o momento de inércia do carretel em relação ao seu centro de massa é .

1. Qual a aceleração do centro de massa do carretel?
2. Determine o módulo da força de atrito que atua no carretel e mostre que ela aponta para a direita.
3. Se o coeficiente de atrito entre o carretel e a superfície é , qual a máxima força que pode ser aplicada ao carretel para que ele continue a rolar sem deslizar.