Um brinquedo comum de criança consiste em duas pequenas esferas de madeira amarradas por um fio, de massa desprezível e comprimento , e que são postas para colidir acima e abaixo do ponto de sustentação. No instante retratado pelo desenho, cada bola tem uma velocidade linear e o fio está esticado. Considere que o eixo de rotação é fixo.
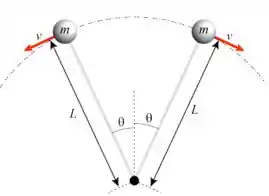
- Desenhe as forças atuando em cada esfera no instante mostrado no desenho.
- Calcule o módulo das acelerações centrípeta e tangencial em cada esfera.
- Qual é a tração no fio neste instante ?
- Calcule os torques da força peso e tração em cada uma das esferas, indicando direção e sentido, em relação ao eixo de rotação fixo.
- Calcule o momento angular de cada bola em relação ao eixo de rotação fixo, e o momento angular total do sistema.
Passo 1
a):
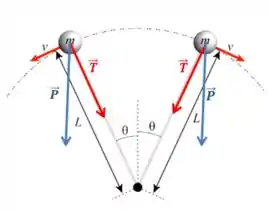
Onde:
Peso.
Tensão.
Passo 2
b):
Calcular o módulo da aceleração centrípeta é fácil, só usar a equação:
Onde:
Então:
Ah, você pensou em calcular fazendo a soma da tensão amis a componente do peso na direção da tensão? Tipo assim:
Bom, até ta certo, mas lembre-se que nós não sabemos o valor de
Na verdade, a gente vai usar esse caminho pra achar mas isso são cenas dos próximos capítulos.
Agora, pra se calcular a aceleração tangencial, basta decompor o peso nessa direção:
Passo 3
c):
Como eu disse, agora vamos usar:
Passo 4
d):
Bom, a tensão em relação ao eixo de rotação não efetua torque, já que ela age na própria direção do fio. Assim:
Isso vale pras duas esferas. Já pro peso, vamos ter que analisar cada uma:
A bolinha da esquerda:
Bem, o peso tem uma componente que efetua um torque e uma que não. A componente na direção da corda, não efetua torque, mas o tangencial sim. A bolinha esquerda no sentido anti-horário, vamos atribuir o valor negativo ao sentido anti-horário, assim:
Beleza?
Pra segunda bolinha:
Nesse caso, a segunda bolinha gira no sentido horário, o que a gente chamou de positivo, então:
Passo 5
e):
Bom galera, o momento angular pode ser escrito como:
Vamos calcular o momento de inércia de uma partícula em relação ao eixo?
É simples assim:
E como sabemos que:
Então:
Pro sentido horário e :
Pro sentido anti-horário. Então:
Particula 1:
E a partícula 2:
Assim, o momento do sistema é:
Resposta
a):
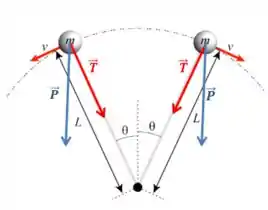
b):
c):