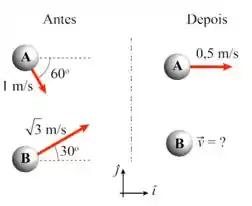
Duas partículas colidem numa superfície sem atrito. As velocidades de ambas antes da colisão são mostradas na figura ao lado. Após a colisão, a partícula A move-se com . Considere que a massa da partícula é o dobro da massa da partícula , ou seja, .
- Qual é a velocidade do centro de massa do sistema antes da colisão?
- Encontre o vetor velocidade da partícula B após a colisão.
- A colisão é elástica? Justifique sua resposta
Passo 1
a):
Nós vamos calcular isso na direção horizontal e vertical.
Mas antes disso, vamos ver, de acordo com os ângulos que a velocidade faz com a horizontal, qual a velocidade que cada uma das partículas tem:
Partícula
E a partícula
Beleza? Agora vamos calcular tanto na horizontal como na vertical, de acordo com a massa de cada uma:
Horizontal:
Agora na vertical:
Vertical:
Então, a velocidade do centro de massa é:
Passo 2
b):
Fazendo o cálculo da conservação de momento na horizontal:
Onde:
Então:
E essa é a velocidade horizontal:
Agora, na vertical:
Onde:
Então:
Passo 3
c):
Pra saber se ela é elástica ou não, vamos calcular a energia cinética antes e depois.
A energia cinética antes da colisão é dada pela soma das energias cinéticas na horizontal e na vertical:
E a energia cinética após a colisão é:
Como:
Então, a energia cinética não se conservou, logo, a colisão não é elástica.
Resposta
a):
b):
c):
A colisão não é elástica.