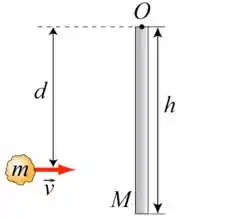
Uma barra homogênea de massa e comprimento pode girar em torno de um eixo fixo (ponto O) em uma de suas extremidades. Uma bola de massa de modelar, com massa e velocidade , atinge a barra a uma distância do eixo e fica grudada na barra. Dado: O momento de inércia e uma haste de massa e comprimento h em relação a um eixo que passa pelo seu centro de massa é

Momento de inércia de uma barra: .

1. Que grandezas são conservadas durante a colisão? Justifique sua resposta.
2. Qual o momento de inércia do sistema bola+barra em relação ao ponto O ?
3. Qual o momento angular do sistema após a colisão em relação ao ponto O ?
4. Qual a razão entre a energia final e a energia inicial do sistema?

b):

Bom, vamos primeiro calcular o momento de inércia da barra em relação ao ponto , usando o teorema dos eixos paralelos:

Quem é esse

É a distância do centro de massa da barra até o ponto então:

Assim:

Beleza?

E qual é o momento de inércia da massinha em relação ao ponto

Onde é a distancia do centro de massa da massinha até o centro

Assim:

c):

Ai a gente tem que usar a conservação do momento angular que diz:

Ou:

Beleza?

Bom, como a gente pode ver, é só calcular o momento inicial. O momento inicial é dado pela rotação da massinha, isso é:

Mas como é perpendicular a , pelo produto vetorial:

Já que:

Show?

Então o módulo do momento inicial é:

Voltando pros vetores:

Então:

E como o final é igual a isso:

d):

Bom, galera, antes da colisão, havia apenas energia cinética de translação da massinha. Após a colisão, existe apenas a energia cinética de rotação do conjunto massa barra.

Assim:

E:

Beleza?

Como calcular a energia inicial é tranquilo, já que todos os dados que estão lá são conhecidos, a gente só precisa descobrir a energia final. Como já sabemos , basta descobrir

Ai a gente pode usar a relação:

Como:

E:

Então:

Assim:

Substituindo o valor de e de

Assim:

Assim:

O que faz sentido! O lado direito da equação é maior que

Ou seja, houve perda de energia na colisão!