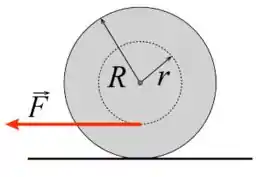
Um carretel de massa e raio externo rola sem deslizar, para a esquerda, ao ser puxado por uma força aplicada ao seu raio interno como mostra a figura. Sabe-se que o momento de inércia do carretel em relação ao seu centro de massa é .
- Qual a aceleração do centro de massa do carretel?
- Determine o módulo da força de atrito que atua no carretel e mostre que ela aponta para a direita.
- Se o coeficiente de atrito entre o carretel e a superfície é , qual a máxima força que pode ser aplicada ao carretel para que ele continue a rolar sem deslizar.
Passo 1
a):
Bom galera, podemos listar três equações que regem esse movimento ai.
Primeiro, como existem forças sendo aplicadas em um corpo, podemos escrever a segunda lei de Newton:
Além disso, existem torques agindo ali também. Tem tanto o torque da força de atrito quanto a da força externa.
No entanto, a gente pode ver pela figura que a força externa faz ele girar no sentido horário. Porém, o enunciado diz que ele rola pra esquerda, o que quer dizer que rolal no sentido anti-horário.
Então é de se esperar que o torque da força de atrito seja maior que o da força externa. Assim:
Beleza?
E por ultimo, já que o carretel rola sem deslizar:
Beleza? Então temos:
Substituindo a terceira na segunda:
Isolando
Guarda essa fórmula!!!!
Agora, substituindo na primeira:
Passo 2
b):
Provar que ela se move no sentido é só você argumentar que, como no final o carretel roda no sentido anti-horário, o torque da força de atrito tem que ser maior que o da força e tem que ter o sentido contrário ao torque de
Beleza?
Pra calcular o módulo a gente substitui aqui:
Passo 3
d):
Beleza galera. Aqui vamos trabalhar com a condição de iminência.
Quando o corpo estiver na condição de iminência de deixar de rolar sem deslizar, as três equações que listamos em a) contnuarão valendo:
Só que ali na primeira equação, vamos chamar de :
E:
A idéia é que ao aplicarmos uma força máxima, vamos gerar uma reação de uma força de atrito máximo no sistema, mas as três equações continuam valendo.
Mas qual o módulo do atrito máximo?
Beleza? Onde:
]Assim:
Assim, substituindo na equação:
Show! Mas quanto vale a aceleração mesmo?
Então:
Resposta
a):
b):
c):