P2 de Física 2- FIS1041 da PUCRIO - 2015.1

Uma onda propaga-se numa corda na direção em sentido negativo com velocidade de . A tração na corda é de . A expressão do deslocamento dos pontos da corda em função do tempo é:

No instante os deslocamentos ao longo de são dados pelo gráfico abaixo.

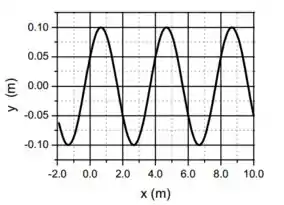
1. Determine a amplitude do deslocamento e o comprimento de onda.
2. Determine o ângulo de fase .
3. Calcule e (deixe em função de e escreva a função para essa onda, escolhendo corretamente o sinal na frente de
4. Obtenha e velocidade transversal dos pontos da corda em função de e
5. Calcule a energia média por unidade de tempo transmitida pela corda.

Um tubo cilíndrico, com uma extremidade aberta e outra fechada, tem um diâmetro e largura . Ele tem ar no seu interior. Suponha que a extremidade fechada do tubo esteja na posição . Considere a velocidade do som igual a .

Um alto-falante, posicionado perto do lado aberto do tubo, emite som numa faixa de frequências de e

1. Calcule em quais frequências emitidas pelo alto-falante o som entra em ressonância no tubo.
2. O alto-falante começa a se afastar de . Calcule a nova faixa de frequências de som que chega ao tubo e diga para quais frequências da fonte o tubo entra em ressonância.

Um tubo cilíndrico, com uma extremidade aberta e outra fechada, tem um diâmetro e largura . Ele tem ar no seu interior. Suponha que a extremidade fechada do tubo esteja na posição . Considere a velocidade do som igual a .

1. Calcule a frequência natural de ressonância do tubo.
2. Para a frequência natural do tubo, considere que, na extremidade aberta do tubo, o deslocamento dos elementos de ar é máximo em e vale . Escreva a função para esse deslocamento no interior do tubo . Faça o gráfico dessa função em .

Duas fontes sonoras ( e), quando ligadas, emitem isotropicamente sons de frequência de no ar. A potência acústica emitida por é igual a Considere um ponto a de e a de .(velocidade do som no ar é igual a ).

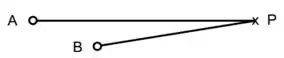
1. A fonte , atuando sozinha, produz em um som de mesma intensidade que a fonte (também atuando sozinha). Calcule a potência acústica de
2. Encontre a diferença de fase das duas ondas que chegam em ( deixei em função de . Diga, justificando, se ocorre interferência construtiva ou destrutiva.
3. Encontre a amplitude dos deslocamentos da onda resultante no ponto.
4. Considere agora que a frequência do som emitido pelas fontes seja . Diga, justificando, que interferência irá ocorrer.
5. Calcule, na situação do item d), a razão entre a intensidade do som em quando e estão ligadas e a intensidade em quando apenas uma fonte está ligada.