Uma onda propaga-se numa corda na direção em sentido negativo com velocidade de . A tração na corda é de . A expressão do deslocamento dos pontos da corda em função do tempo é:
No instante os deslocamentos ao longo de são dados pelo gráfico abaixo.
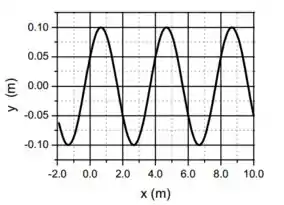
- Determine a amplitude do deslocamento e o comprimento de onda.
- Determine o ângulo de fase .
- Calcule e (deixe em função de e escreva a função para essa onda, escolhendo corretamente o sinal na frente de
- Obtenha e velocidade transversal dos pontos da corda em função de e
- Calcule a energia média por unidade de tempo transmitida pela corda.
Passo 1
a):
Galera, a gente pode descobrir isso analisando o gráfico. Pelo gráfico, os ciclos se repetem a cada , logo, esse é o comprimento de onda.
Você pode ver, por exemplo, o ponto e o ponto . Os dois tem
E a amplitude é o máximo valor de . O maior valor disso vai ser o valor de um pico, e como dá pra ver ali no gráfico, esse valor é
Passo 2
b):
A fórmula de segue o padrão de uma equação de onda, ou seja:
Então, em e
Po, mas pelo gráfico, o valor de é:
Passo 3
c):
Pra calcular é fácil, já que já temos o valor de
E pra achar , vamos usar a relação:
Passo 4
d):
A velocidade transversal é derivada parcial da função posição em relação ao tempo, lembra?
Mas antes, vamos escrever a função , já que já temos todas as informações:
Então:
Passo 5
e):
E energia por unidade de tempo é a potência. A gente vai usar aquela velha fórmula:
Temos quase tudo, menos a densidade linear. Então:
Então:
Resposta
a):
b):
c):
d):
e):