P2 de Física 2- FIS1041 da PUCRIO - 2017.2

Um pulso numa corda é descrito pela função:

Onde são dados em cm e t em segundos.

a) Calcule a velocidade do pulso e determine em que sentido ele se propaga.

b) Determine a velocidade dos pontos da corda em função de x e t e calcule essa velocidade em x = 0 e t = 0.

c) Encontre uma função de onda que descreva o pulso de mesma forma mas que se propaga em sentido oposto.

Uma corda de violino de 30 cm de comprimento com uma massa específica linear de 0,65 g/m é colocada perto de um alto-falante alimentado por um oscilador de áudio de frequência variável. Observa-se que a corda entra em oscilação apenas nas frequências de 880 Hz e 1320 Hz, quando a frequência do oscilador de áudio varia no intervalo de 500 a 1500 Hz.

a) Determine a que harmônicos correspondem as frequências de 880 e 1320 Hz e faça um esboço da forma de oscilação da corda nesses dois modos.

b) Determine a tensão na corda.

Um alto falante, mostrado na figura abaixo, que emite um sinal sonoro com frequência de 440 Hz, foi conectado a um sistema massa-mola. O sistema realiza um movimento harmônico simples com velocidade máxima de 6 m/s e amplitude de oscilação de 0,5 m. O alto falante se move para a direita e para a esquerda, se aproximando e se afastando de um ouvinte que se encontra em repouso.

A separação mínima entre o ouvinte e o alto falante é de 1,5 m. Considere o alto falante uma fonte pontual isotrópica.

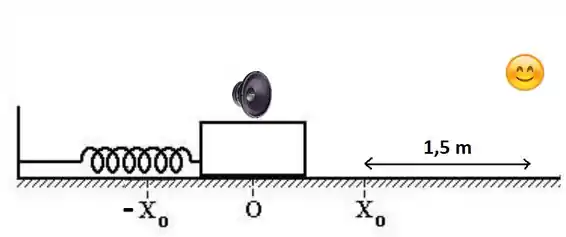
a) Determine a maior e a menor frequência detectada pelo ouvinte.

Considere em seguida que o nível sonoro máximo detectado pelo ouvinte é de 60 dB, quando a fonte está mais próxima do ouvinte.

b) A intensidade do som na posição do ouvinte, em W/m2, quando o alto falante estiver mais próximo do ouvinte;

c) A potência do alto falante;

d) O nível sonoro, em dB, quando o alto falante estiver na posição mais afastada possível do ouvinte.

Uma onda transversal senoidal com um comprimento de onda de 80 cm propaga-se no sentido positivo de um eixo x. A figura abaixo mostra a velocidade transversal da partícula situada em x = 0 em função do tempo.

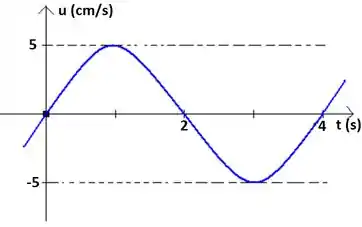
a) Determine a frequência e a velocidade de propagação da onda.

b) Determine a amplitude da onda (máximo deslocamento das partículas).

c) Determine a função de onda y(x,t) e faça o gráfico entre x = 0 e x = 80 cm no instante t = 2 s.

Considere agora que a onda acima se superponha a outra onda com a mesma frequência e mesma amplitude, mas com uma diferença de fase em relação a ela.

d) Encontre a diferença de fase para que a taxa média de energia transportada pela onda resultante seja o dobro da transportada por cada onda, separadamente.